Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T16:06:07.456Z Has data issue: false hasContentIssue false
  • English
  • Français

Isometry on Linear n-G-quasi Normed Spaces

Published online by Cambridge University Press:  20 November 2018

Yumei Ma
Yumei Ma*
Affiliation:
Department of Mathematics, Dalian Nationalities University, 116600 Dalian, China. mayumei@dlnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

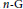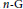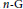This paper generalizes the Aleksandrov problem: the Mazur-Ulam theorem on $n-G$-quasi normed spaces. It proves that a one-$n$-distance preserving mapping is an $n$-isometry if and only if it has the zero-$n-G$-quasi preserving property, and two kinds of $n$-isometries on $n-G$-quasi normed space are equivalent; we generalize the Benz theorem to $n$-normed spaces with no restrictions on the dimension of spaces.

Keywords

46B2046B0451K05n-G-quasi normMazur–Ulam theoremAleksandrov problemn-isometryn-0-distance
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 2 , 01 June 2017 , pp. 350 - 363
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Aleksandrov, A. D., Mappings of families of sets. Dokl. Akad. Nauk SSSR 191(1970), 503–506. Google Scholar
[2] Benz, W., A contribution to a theorem ofUlam and Mazur. Aequationes Math. 34(1987), 61–63. http://dx.doi.org/1 0.1007/BF01 840123 Google Scholar
[3] Chu, H., Choi, S., and Kang, D., Mapping of conservative distances in linear n-normed spaces. Nonlinear Anal. 70(2009), no. 3,1168-1174. http://dx.doi.org/10.1016/j.na.2OO8.O2.002 Google Scholar
[4] Chu, H., Lee, K., and Park, C., On the Aleksandrov problem in linear n-normed spaces. Nonlinear Anal. 59(2004), no. 7,1001-1011. Google Scholar
[5] Ekariani, S., Gunawan, H., and Idris, M., A contractive mapping theorem on the n-normed space of p-summable sequences. J. Math. Anal. 4(2013) 1–7. Google Scholar
[6] Gao, J., On the Aleksandrov problem of distance preserving mapping. J. Math. Anal. Appl. 352(2009), no. 2, 583–590. http://dx.doi.org/10.1016/j.jmaa.2008.10.022 Google Scholar
[7] Gehér, G. P., On n-norm preservers and the Aleksandrov conservative n-distance problem. arxiv:1 507.05046 Google Scholar
[8] Jing, Y., The Aleksandrov problem in p-normed spaces (0 <p < 1). Acta Sci. Nat. Univ. Nankai. 4(2008), 91–96. Google Scholar
[9] Mazur, S. and Ulam, S., Sur les transformationes isométriques d'espaces vectoriels normes. C. R. Acad. Sci. Paris. 194(1932), 946–948. Google Scholar
[10] Ma, Y., The Aleksandrov problem for unit distance preserving mapping. Acta Math. Sci. Ser. B Engl. Ed. 20(2000), no. 3, 359–364.Google Scholar
[11] Ma, Y., The Aleksandrov problem and The Mazur- Ulam theorem on linear n-normed space. Bull. Korean Math. Soc. 50(2013), no. 5, 1631–1637. http://dx.doi.org/10.4134/BKMS.2013.50.5.1631 Google Scholar
[12] Ma, Y., Isometry on linear n-normed spaces. Ann. Acad. Sci. Fenn. Math. 39(2014),no. 2, 973–981. http://dx.doi.org/10.5186/aasfm.2014.3941 Google Scholar
[13] Ma, Y., The Aleksandrov-Benz-Rassias problem on linear n-normed spaces, Monatsh. Math. 180(2016), 305–316. http://dx.doi.org/!0.1007/s00605-015-0786-8 Google Scholar
[14] Park, C. and Alaca, C., Anew version ofMazur- Ulam theorem under weaker conditions in linear n-normed spaces. J. Comput. Anal. Appl. 16(2014), no. 5, 827–832. Google Scholar
[15] Park, C. and Rassias, T. M., Isometries on linear n-normed spaces. JIPAM. J. Inequal. Pure Appl. Math. 7(2006), Article 168, 7 pp. (electronic).Google Scholar
[16] Park, C. and Rassias, T. M., Isometric additive in generalized quasi-Banach spaces. Banach J. Math. Anal. 2(2008), no. 1, 59–69. http://dx.doi.org/10.15352/bjma/1240336274 Google Scholar
[17] Rassias, T. M. and Semrl, P., On the Mazur-Ulam theorem and the Aleksandrov problem for unit distance preserving mappings. Proc. Amer. Math. Soc. 132(1993), no. 3, 919–925. http://dx.doi.org/10.1090/S0002-9939-1993-1111437-6 Google Scholar
[18] Yunchen, X. and Meimei, S., Characterizations on isometries in linear n-normed spaces. Nonlinear Anal. 72(2010), 1895–1901. http://dx.doi.org/10.1016/j.na.2009.09.029 Google Scholar
[19] Zheng, F. and Ren, W. The Aleksandrov problem in quasi convex normed linear space. Acta Sci. Natur. Nankai Univ. 47(2014), no. 3, 49–56.Google Scholar