Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-11T01:06:15.630Z Has data issue: false hasContentIssue false
  • English
  • Français

James-Hopf Invariants, Anick’s Spaces, and the Double Loops on Odd Primary Moore Spaces

Published online by Cambridge University Press:  20 November 2018

Joseph Neisendorfer
Joseph Neisendorfer*
Affiliation:
University of Rochester Rochester, New York U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using spaces introduced by Anick, we construct a decomposition into indecomposable factors of the double loop spaces of odd primary Moore spaces when the powers of the primes are greater than the first power. If $n$ is greater than 1, this implies that the odd primary part of all the homotopy groups of the 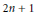$2n\,+\,1$ dimensional sphere lifts to a mod 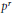${{p}^{r}}$ Moore space.

Keywords

55Q5255P35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 2 , 01 June 2000 , pp. 226 - 235
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Anick, D., Differential Algebras in Topology. Res. Notes Math. 3, A.K. Peters Ltd., 1993.Google Scholar
[2] Anick, D. and Gray, B., Small H spaces related to Moore spaces. Topology 43(1995), 859–881.Google Scholar
[3] Cohen, F. R. and Mahowald, M. E., A remark on self-maps of Ω2S2n+1 . Indiana Univ. Math J. 30(1981), 583–588.Google Scholar
[4] Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., Torsion in homotopy groups. Ann. of Math. 109(1979), 121–168.Google Scholar
[5] Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., The double suspension and exponents of the homotopy groups of spheres. Ann. of Math. 110(1979), 549–565.Google Scholar
[6] Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., Exponents in homotopy theory. In: Algebraic Topology and Algebraic K-theory (ed. Browder, W.), Princeton Univ. Press, 1987.Google Scholar
[7] James, I. M., Reduced product spaces. Ann. of Math. 62(1955), 170–197.Google Scholar
[8] James, I. M., On the suspension sequence. Ann. of Math. 65(1957), 74–107.Google Scholar
[9] Neisendorfer, J. A., Properties of certain H-spaces. Quart. Math, J..Oxford Ser. (2) 34(1983), 201–209.Google Scholar
[10] Neisendorfer, J. A., The exponent of a Moore space. In: Algebraic Topology and Algebraic K-theory (ed. Browder, W.), Princeton Univ. Press, 1987.Google Scholar
[11] Neisendorfer, J. A., Product decompositions of the double loops on odd primary Moore spaces. Topology, to appear.Google Scholar
[12] Selick, P. S., Odd primary torsion in πK(S3). Topology 17(1978), 407–412.Google Scholar
[13] Theriault, S. D., A reconstruction of Anick's fibration, University of Toronto Thesis, 1997.Google Scholar
[14] Theriault, S. D., Properties of Anick's Spaces. Preprint.Google Scholar