Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T15:45:38.127Z Has data issue: false hasContentIssue false
  • English
  • Français

Jordan *-Derivations of Finite-DimensionalSemiprime Algebras

Published online by Cambridge University Press:  20 November 2018

Ajda Fošner  and
Tsiu-Kwen Lee
Ajda Fošner
Affiliation:
Faculty of Management, University of Primorska, Cankarjeva 5, SI-6104 Koper, Slovenia e-mail: ajda.fosner@fm-kp.si
Tsiu-Kwen Lee*
Affiliation:
Department of Mathematics, National Taiwan University, Taipei 106, Taiwan e-mail: tklee@math.ntu.edu.tw
*
Corresponding author: Tsiu-Kwen Lee. T.-K. Lee was supported by NSC and NCTS/TPE of Taiwan.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we characterize Jordan $*$-derivations of a 2-torsion free, finite-dimensional semiprime algebra $R$ with involution $*$. To be precise, we prove the following. Let $\delta :\,R\,\to \,R$ be a Jordan $*$-derivation. Then there exists a $*$-algebra decomposition $R\,=\,U\,\oplus \,V$ such that both 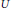$U$ and 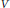$V$ are invariant under $\delta $. Moreover, $*$ is the identity map of 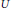$U$ and 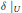$\delta {{|}_{U}}$ is a derivation, and the Jordan $*$-derivation 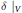$\delta {{|}_{V}}$ is inner. We also prove the following. Let $R$ be a noncommutative, centrally closed prime algebra with involution $*$, char 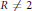$R\,\ne \,2$, and let $\delta $ be a nonzero Jordan $*$-derivation of $R$. If $\delta $ is an elementary operator of $R$, then 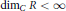${{\dim}_{C}}\,R\,<\,\infty $ and $\delta $ is inner.

Keywords

16W1016N6016W25semiprime algebrainvolution(inner) Jordan *-derivationelementary operator
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 51 - 60
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Bergen, J., Derivations in prime rings. Canad. Math. Bull. 26 (1983), no. 3, 267–270. http://dx.doi.org/10.4153/CMB-1983-042-2 Google Scholar
[2] Brešar, M. and Vukman, J., On some additive mappings in rings with involution. Aequationes Math. 38 (1989), no. 2–3, 178–185. http://dx.doi.org/10.1007/BF01840003 Google Scholar
[3] Brešar, M. and Zalar, B., On the structure of Jordan *-derivations. Colloq. Math. 63 (1992), no. 2, 163–171.Google Scholar
[4] Chuang, C.-L., Fošner, A., and Lee, T.-K., Jordan *-derivations of locally matrix rings. Algebr. Represent. Theory, published online December 15, 2011, http://dx.doi.org/10.1007/s10468-011-9329-8. Google Scholar
[5] Herstein, I. N., Topics in ring theory. The University of Chicago Press, Chicago, Ill.-London, 1969.Google Scholar
[6] Jacobson, N., PI-algebras. An introduction. Lecture Notes in Mathematics, 441, Springer-Verlag, Berlin-New York, 1975.Google Scholar
[7] Jacobson, N. and Rickart, C. E., Jordan homomorphisms of rings. Trans. Amer. Math. Soc. 69 (1950), 479–502.Google Scholar
[8] Lee, T.-K., Finiteness properties of differential polynomials. Linear Algebra Appl. 430 (2009), no. 8–9, 2030–2041. http://dx.doi.org/10.1016/j.laa.2008.11.007 Google Scholar
[9] Martindale, W. S. III, Prime rings satisfying a generalized polynomial identity. J. Algebra 12 (1969), 576–584. http://dx.doi.org/10.1016/0021-8693(69)90029-5 Google Scholar
[10] Šemrl, P., Jordan*-derivations on standard operator algebras. Proc. Amer. Math. Soc. 120 (1994), no. 2, 515–518.Google Scholar