Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-13T09:23:46.753Z Has data issue: false hasContentIssue false
  • English
  • Français

Least Positive Residues and the Quadratic Character of Two

Published online by Cambridge University Press:  20 November 2018

Kenneth H. Rosen
Kenneth H. Rosen*
Affiliation:
Department of Mathematics University of Colorado Boulder, Colorado 80309 USA Department of Mathematics The University of Maine Orond, Maine, 04469 USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 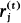be the least positive residue modulo 2tk of (2j- l)h. Define ut to be the number of 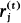with l≤j≤2t-2k such that 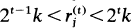. At the Special Session in Combinatorial Number Theory at the 1977 Summer AMS Meeting Szekeres [2] asked for a simple proof that if (h, 2k)=1, then

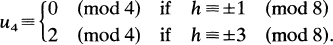
Here a simple proof will be given for the following equivalent result.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 3 , 01 September 1980 , pp. 355 - 358
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Bachmann, P., Die Elemente der Zahlentheorie, Teubner, Leipzig, 1892, (reprint: Chelsea, New York, 1968), p. 144-148.Google Scholar
2. Long, C., Problem List, Combinatorial Number Theory, Notices of the American Mathematical Society, 25 (1978), p. 145.Google Scholar