Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gross, Benedict H.
and
McMullen, Curtis T.
2002.
Automorphisms of even unimodular lattices and unramified Salem numbers.
Journal of Algebra,
Vol. 257,
Issue. 2,
p.
265.
Silver, Daniel S
Stoimenow, Alexander
and
Williams, Susan G
2006.
Euclidean Mahler measure and twisted links.
Algebraic & Geometric Topology,
Vol. 6,
Issue. 2,
p.
581.
Kadokami, Teruhisa
and
Yamada, Yuichi
2007.
A deformation of the Alexander polynomials of knots yielding lens spaces.
Bulletin of the Australian Mathematical Society,
Vol. 75,
Issue. 1,
p.
75.
Akiyama, Shigeki
and
Kwon, Do Yong
2008.
Constructions of Pisot and Salem numbers with flat palindromes.
Monatshefte für Mathematik,
Vol. 155,
Issue. 3-4,
p.
265.
Hironaka, Eriko
2010.
Small dilatation mapping classes coming from the simplest hyperbolic braid.
Algebraic & Geometric Topology,
Vol. 10,
Issue. 4,
p.
2041.
Kellerhals, Ruth
and
Perren, Geneviève
2011.
On the growth of cocompact hyperbolic Coxeter groups.
European Journal of Combinatorics,
Vol. 32,
Issue. 8,
p.
1299.
CLAY, ADAM
and
ROLFSEN, DALE
2012.
Ordered groups, eigenvalues, knots, surgery and L-spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 152,
Issue. 1,
p.
115.
Kellerhals, Ruth
2013.
Cofinite hyperbolic Coxeter groups, minimal growth rate and Pisot numbers.
Algebraic & Geometric Topology,
Vol. 13,
Issue. 2,
p.
1001.
Kellerhals, Ruth
and
Kolpakov, Alexander
2014.
The Minimal Growth Rate of Cocompact Coxeter Groups in Hyperbolic 3-space.
Canadian Journal of Mathematics,
Vol. 66,
Issue. 2,
p.
354.
Smyth, Chris
2015.
Seventy years of Salem numbers.
Bulletin of the London Mathematical Society,
Vol. 47,
Issue. 3,
p.
379.
McMullen, Curtis T.
2016.
Automorphisms of projective K3 surfaces with minimum entropy.
Inventiones mathematicae,
Vol. 203,
Issue. 1,
p.
179.
Bucher, Michelle
and
Talambutsa, Alexey
2016.
Exponential growth rates of free and amalgamated products.
Israel Journal of Mathematics,
Vol. 212,
Issue. 2,
p.
521.
Stoimenov, Alexander
2019.
Knots, Low-Dimensional Topology and Applications.
Vol. 284,
Issue. ,
p.
191.
Nie, Zipei
2019.
Left-orderablity for surgeries on (−2,3,2s + 1)-pretzel knots.
Topology and its Applications,
Vol. 261,
Issue. ,
p.
1.
Vieira, Ricardo
2019.
Polynomials - Theory and Application.
Teragaito, Masakazu
2022.
Hyperbolic L-space knots and their formal semigroups.
International Journal of Mathematics,
Vol. 33,
Issue. 12,
Motegi, Kimihiko
and
Teragaito, Masakazu
2022.
Generalized torsion for knots with arbitrarily high genus.
Canadian Mathematical Bulletin,
Vol. 65,
Issue. 4,
p.
867.
Chinburg, Ted
Reid, Alan W
and
Stover, Matthew
2022.
Azumaya Algebras and Canonical Components.
International Mathematics Research Notices,
Vol. 2022,
Issue. 7,
p.
4969.
Tange, Motoo
2023.
Upsilon invariants of L-space cable knots.
Topology and its Applications,
Vol. 324,
Issue. ,
p.
108335.
KELLERHALS, R.
and
LIECHTI, L.
2023.
SALEM NUMBERS, SPECTRAL RADII AND GROWTH RATES OF HYPERBOLIC COXETER GROUPS.
Transformation Groups,
Vol. 28,
Issue. 2,
p.
831.
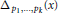 ${{\Delta }_{p1,...,{{p}_{k}}\left( x \right)}}$ of pretzel knots and links with
${{\Delta }_{p1,...,{{p}_{k}}\left( x \right)}}$ of pretzel knots and links with 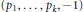 $\left( {{p}_{1}},...,{{p}_{k}},-1 \right)$ twists, where
$\left( {{p}_{1}},...,{{p}_{k}},-1 \right)$ twists, where 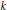 $k$ is odd and
$k$ is odd and 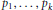 ${{p}_{1}},...,{{p}_{k}}$ are positive integers. The polynomial
${{p}_{1}},...,{{p}_{k}}$ are positive integers. The polynomial 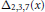 ${{\Delta }_{2,3,7}}\left( x \right)$ is the well-known Lehmer polynomial, which is conjectured to have the smallest Mahler measure among all monic integer polynomials. We confirm that
${{\Delta }_{2,3,7}}\left( x \right)$ is the well-known Lehmer polynomial, which is conjectured to have the smallest Mahler measure among all monic integer polynomials. We confirm that 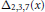 ${{\Delta }_{2,3,7}}\left( x \right)$ has the smallest Mahler measure among the polynomials arising as
${{\Delta }_{2,3,7}}\left( x \right)$ has the smallest Mahler measure among the polynomials arising as 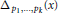 ${{\Delta }_{p1,...,{{p}_{k}}\left( x \right)}}$.
${{\Delta }_{p1,...,{{p}_{k}}\left( x \right)}}$.

