Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T10:02:36.651Z Has data issue: false hasContentIssue false
  • English
  • Français

L-functions for Quadratic Characters and Annihilation of Motivic Cohomology Groups

Published online by Cambridge University Press:  20 November 2018

Jonathan W. Sands
Jonathan W. Sands*
Affiliation:
Department of Mathematics and Statistics, University of Vermont, Burlington, VT 25401, USA e-mail: jonathan.sands@uvm.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 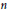$n$ be a positive even integer, and let 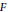$F$ be a totally real number field and $L$ be an abelian Galois extension which is totally real or 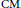$\text{CM}$ . Fix a finite set $S$ of primes of 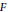$F$ containing the infinite primes and all those which ramify in $L$ , and let 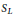${{S}_{L}}$ denote the primes of $L$ lying above those in $S$ . Then 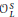$\mathcal{O}_{L}^{S}$ denotes the ring of 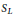${{S}_{L}}$ -integers of $L$ . 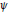Suppose that $\psi$ is a quadratic character of the Galois group of $L$ over 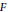$F$ . Under the assumption of the motivic Lichtenbaum conjecture, we obtain a non-trivial annihilator of the motivic cohomology group 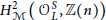$H_{\mathcal{M}}^{2}\left( \mathcal{O}_{L}^{S},\mathbb{Z}\left( n \right) \right)$ from the lead term of the Taylor series for the S-modified Artin $L$ -function $L_{L/F}^{S}\left( s,\psi\right)$ at $s=1-n$ .

Keywords

11R4211R7014F4219F27motivic cohomologyregulatorArtin L-functions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 620 - 631
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Burns, D., On derivatives ofArtin L-series. Invent. Math. 186(2011), 291–371. http://dx.doi.Org/1 0.1 007/S00222-011 -0320-0 Google Scholar
[2] Geisser, T., Motivic cohomology over Dedekind rings. Math. Z. 248(2004), 773–875. http://dx.doi.Org/1 0.1 007/s00209-004-0680-x Google Scholar
[3] Junkins, C. and Kolster, M., The analogue of the Gauss class number problem in motivic cohomology, Ann. Sci. Math. Quebec 36(2012), 69–96. http://dx.doi.Org/1 0.1 007/S4031 6-01 3-0006-7 Google Scholar
[4] Kolster, M., Cohomological version of the Lichtenbaum conjecture at the prime 2.Appendix in: Rognes, J. and Weibel, C., Two-primary algebraic K-theory of rings of integers in number fields. J. Amer. Math. Soc. 13(2000), 1–54. http://dx.doi.Org/1 0.1 090/S0894-0347-99-0031 7-3 Google Scholar
[5] Kolster, M., K-theory and Arithmetic. In: Contemporary developments in algebraic Jf-theory, ICTP Lecture Notes XV, Abdus Salam Int. Cent. Theoret. Phys., Trieste, 2004, 191–258.Google Scholar
[6] Kolster, M., Nguyen Quang-Do, T., and Fleckinger, V., Twisted S-units, p-adic class number formulas, and the Lichtenbaum conjectures. Duke Math. J. 84(1996), 679–717. http://dx.doi.Org/1 0.1 21 5/S0012-7094-96-08421 -5 Google Scholar
[7] Neukirch, J., The Beilinson conjecture for algebraic number fields.In: Beilinson's Conjectures on Special Values of L-Functions, Perspect.Math. 4, Academic Press, San Diego, 1988, 193–248.Google Scholar
[8] Nickel, A., Leading terms ofArtin L-series at negative integers and annihilation of higher K-groups. Math. Proc. Camb. Philos. Soc. 151(2011), 1–22. http://dx.doi.Org/1 0.1 01 7/S0305004111 0001 93 Google Scholar
[9] Sands, J. W. L-functions at the origin and annihilation of class groups in multiquadratic extensions. Acta Arithmetica 154(2012), 173–185. http://dx.doi.Org/1 0.4064/aa1 54-2-5 Google Scholar
[10] Sands, J. W. and Simons, L. D., Values at s =-1 oj “L-functions for multi-quadratic extensions of number fields and annihilation of the tame kernel. J London Math. Soc. 76(2007), 545–555. http://dx.doi.Org/10.111 2/jlms/jdmO74 Google Scholar
[11] Snaith, V. P., Stark's conjectures and new Stickelberger phenomena. Canad. J. Math. 58(2006), 419–448. http://dx.doi.Org/1 0.41 53/CJM-2006-01 8-5 Google Scholar
[12] Tate, J. T., Symbols in Arithmetic. In: Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1, Gauthier-Villars, 1971, 201–211.Google Scholar
[13] Tate, J. T. Les conjectures de Stark sur les fonctions L d'Artin en s = 0. Birkhauser, Boston, 1984.Google Scholar
[14] Voevodsky, V., Onmotiviccohomology with Z/l-coefficients. Ann. of Math. 174(2011), 401–438. http://dx.doi.Org/1 0.4007/annals.2011.1 74.1.11 Google Scholar
[15] Wiles, A., The Iwasawa conjecture for totally real fields. Ann. of Math. 131(1990), 493–540. http://dx.doi.Org/1 0.2307/1 971468 Google Scholar