Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T07:48:37.085Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Functionals on Homogeneous Polynomials

Published online by Cambridge University Press:  20 November 2018

Charles F. Dunkl
Charles F. Dunkl*
Affiliation:
University of Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The space Hm of homogeneous polynomials in n real variables x1, x2,…, xn of degree m may be considered as an inner product space with inner product 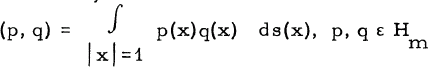; where ds is the rotation-invariant measure on Sn-1 = {x ε Rn: |x| = 1}, 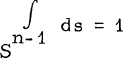. The problem solved in this paper is the following: given n-1 a linear functional ϕ on Hm, find Pϕ ε Hm so that ϕ(p) = (p, Pϕ) for all p ε Hm.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 3 , August 1968 , pp. 465 - 468
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Dunkl, C.F., Operators and harmonic analysis on the sphere. Trans. A. M. S. 125 (1966) 250-263. Google Scholar
2. Hua, L.K., harmonic analysis of functions of several complex variables in the classical domains. Translation of mathematical monographs. (A. M.S. Providence, 1963).Google Scholar