No CrossRef data available.
Article contents
Linear independence of series related to the Thue–Morse sequence along powers
Published online by Cambridge University Press: 06 March 2024
Abstract
The Thue–Morse sequence 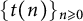 $\{t(n)\}_{n\geqslant 0}$ is the indicator function of the parity of the number of ones in the binary expansion of nonnegative integers n, where
$\{t(n)\}_{n\geqslant 0}$ is the indicator function of the parity of the number of ones in the binary expansion of nonnegative integers n, where  $t(n)=1$ (resp.
$t(n)=1$ (resp. 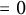 $=0$) if the binary expansion of n has an odd (resp. even) number of ones. In this paper, we generalize a recent result of E. Miyanohara by showing that, for a fixed Pisot or Salem number
$=0$) if the binary expansion of n has an odd (resp. even) number of ones. In this paper, we generalize a recent result of E. Miyanohara by showing that, for a fixed Pisot or Salem number 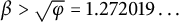 $\beta>\sqrt {\varphi }=1.272019\ldots $, the set of the numbers
$\beta>\sqrt {\varphi }=1.272019\ldots $, the set of the numbers 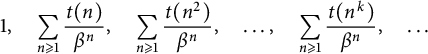 $$\begin{align*}1,\quad \sum_{n\geqslant1}\frac{t(n)}{\beta^{n}},\quad \sum_{n\geqslant1}\frac{t(n^2)}{\beta^{n}},\quad \dots, \quad \sum_{n\geqslant1}\frac{t(n^k)}{\beta^{n}},\quad \dots \end{align*}$$
$$\begin{align*}1,\quad \sum_{n\geqslant1}\frac{t(n)}{\beta^{n}},\quad \sum_{n\geqslant1}\frac{t(n^2)}{\beta^{n}},\quad \dots, \quad \sum_{n\geqslant1}\frac{t(n^k)}{\beta^{n}},\quad \dots \end{align*}$$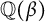 $\mathbb {Q}(\beta )$, where
$\mathbb {Q}(\beta )$, where 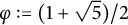 $\varphi :=(1+\sqrt {5})/2$ is the golden ratio. Our result yields that for any integer
$\varphi :=(1+\sqrt {5})/2$ is the golden ratio. Our result yields that for any integer 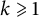 $k\geqslant 1$ and for any
$k\geqslant 1$ and for any 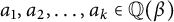 $a_1,a_2,\ldots ,a_k\in \mathbb {Q}(\beta )$, not all zero, the sequence {
$a_1,a_2,\ldots ,a_k\in \mathbb {Q}(\beta )$, not all zero, the sequence {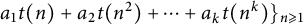 $a_1t(n)+a_2t(n^2)+\cdots +a_kt(n^k)\}_{n\geqslant 1}$ cannot be eventually periodic.
$a_1t(n)+a_2t(n^2)+\cdots +a_kt(n^k)\}_{n\geqslant 1}$ cannot be eventually periodic.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
This work was supported by the Research Institute for Mathematical Sciences, an International Joint Usage/Research Center located in Kyoto University. This research was partly supported by JSPS KAKENHI Grant Number JP22K03263.


