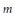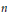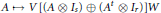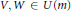Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cheung, Wai-Shun
Li, Chi-Kwong
and
Poon, Yiu-Tung
2004.
Isometries between matrix algebras.
Journal of the Australian Mathematical Society,
Vol. 77,
Issue. 1,
p.
1.
Li, Chi-Kwong
Poon, Yiu-Tung
and
Sze, Nung-Sing
2004.
Isometries for Ky Fan norms between matrix spaces.
Proceedings of the American Mathematical Society,
Vol. 133,
Issue. 2,
p.
369.
Li, Chi-Kwong
and
Sze, Nung-Sing
2004.
Linear maps transforming H-unitary matrices.
Linear Algebra and its Applications,
Vol. 377,
Issue. ,
p.
111.
Cao, Chong-Guang
and
Zhang, Xian
2005.
Linear preservers between matrix modules over connected commutative rings.
Linear Algebra and its Applications,
Vol. 397,
Issue. ,
p.
355.
Zhang, Xian
and
Cao, Chong-guang
2006.
Linear k-power/k-potent preservers between matrix spaces.
Linear Algebra and its Applications,
Vol. 412,
Issue. 2-3,
p.
373.
Yao, Hong Mei
Cao, Chong Guang
and
Zhang, Xian
2009.
Additive preservers of idempotence and Jordan homorphisms between rings of square matrices.
Acta Mathematica Sinica, English Series,
Vol. 25,
Issue. 4,
p.
639.
Petek, Tatjana
and
Radić, Gordana
2022.
Preservers of unitary group or equivalence by unitaries.
Linear Algebra and its Applications,
Vol. 633,
Issue. ,
p.
1.