Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T23:31:43.384Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Operators Preserving Generalized Numerical Ranges and Radii on Certain Triangular Algebras of Matrices

Published online by Cambridge University Press:  20 November 2018

Wai-Shun Cheung  and
Chi-Kwong Li
Wai-Shun Cheung
Affiliation:
Department of Mathematics and Statistics University of Victoria Victoria, B.C. V8W 3P4, e-mail: wshun@math.uvic.ca
Chi-Kwong Li
Affiliation:
Department of Mathematics College of William and Mary P.O. Box 8795 Williamsburg, Virginia 23187-8795 USA, e-mail: ckli@math.wm.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 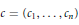$c\,=\,\left( {{c}_{1}},\ldots ,{{c}_{n}} \right)$ be such that 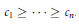${{c}_{1}}\,\ge \,\cdots \,\ge \,{{c}_{n}}$. The 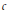$c$-numerical range of an 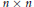$n\,\times \,n$ matrix 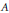$A$ is defined by

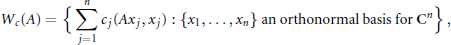$${{W}_{c}}\left( A \right)\,=\,\left\{ \sum\limits_{j=1}^{n}{{{c}_{j}}\left( A{{x}_{j}},\,{{x}_{j}} \right)\,:\,\left\{ {{x}_{1}},\ldots ,{{x}_{n}} \right\}\,\text{an}\,\text{orthonormal basis for }{{\mathbf{C}}^{n}}} \right\}\,,$$

and the 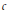$c$-numerical radius of 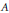$A$ is defined by 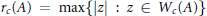${{r}_{c}}\left( A \right)\,=\,\max \left\{ \left| z \right|\,:\,z\,\in \,{{W}_{c}}\left( A \right) \right\}$. We determine the structure of those linear operators 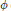$\phi$ on algebras of block triangular matrices, satisfying

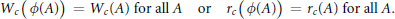$${{W}_{c}}\left( \phi \left( A \right) \right)={{W}_{c}}\left( A \right)\text{for}\,\,\text{all}\,\,A\,\text{or}\,\,{{r}_{c}}\left( \phi \left( A \right) \right)={{r}_{c}}\left( A \right)\text{for}\,\,\text{all}\,A.$$

Keywords

15A0415A6047B49linear operatornumerical range (radius)block triangular matrices
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 3 , 01 September 2001 , pp. 270 - 281
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Chan, J. T., Numerical radius preserving operators on B(H). Proc. Amer. Math. Soc. 123 (1995), 1437–1439.Google Scholar
[2] Chan, J. T., Numerical radius preserving operators on C*-algebras. Arch. Math. (Basel) 70 (1998), 486–488.Google Scholar
[3] Chooi, W. L. and Lim, M. H., Linear preservers on triangular matrices. Linear Algebra Appl. 269 (1998), 241–255.Google Scholar
[4] Horn, R. A. and Johnson, C. R., Topics in Matrix Analysis. Cambridge University Press, New York, 1991.Google Scholar
[5] Li, C. K., Linear operators preserving the numerical radius of matrices. Proc. Amer.Math. Soc. 99 (1987), 601–608.Google Scholar
[6] Li, C. K., Šemrl, P. and Soares, G., Linear operators preserving the numerical range (radius) on triangular matrices. Linear Algebra Appl., to appear. Preprint available at http://www.math.wm.edu/∼ckli/pub.html.Google Scholar
[7] Li, C. K. and Tsing, N. K., Duality between some linear preserver problems: The invariance of the C-numerical range, the C-numerical radius and certain matrix sets. Linear and Multilinear Algebra 23 (1988), 353–362.Google Scholar
[8] Marcoux, L. W. and Sourour, A. R., Commutativity preserving linear maps and Lie automorphisms of triangular matrix algebras. Linear Algebra Appl. 288 (1999), 89–104.Google Scholar
[9] Molnár, L. and Šemrl, P., Some linear preserver problems on upper triangular matrices. Linear and Multilinear Algebra 45 (1998), 189–206.Google Scholar
[10] Omladič, M., On operators preserving the numerical range. Linear Algebra Appl. 134 (1990), 31–51.Google Scholar
[11] Pellegrini, V., Numerical range preserving operators on a Banach algebra. Studia Math. 54 (1975), 143–147.Google Scholar
[12] Poon, Y. T., Another proof of a result of Westwick. Linear and Multilinear Algebra 9 (1980), 181–186.Google Scholar
[13] Pierce, S. et. al., A survey of linear preserver problems. Linear and Multilinear Algebra 33 (1992), 1–129.Google Scholar
[14] Tam, B. S., A simple proof of the Goldberg-Straus theorem on numerical radii. Glasgow Math. J. 28 (1986), 139–141.Google Scholar
[15] Westwick, R., A theorem on numerical ranges. Linear and Multilinear Algebra 2 (1975), 311–315.Google Scholar