Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T17:46:02.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Relations Among the Values of Canonical Heights from the Existence of Non-Trivial Endomorphisms

Published online by Cambridge University Press:  20 November 2018

Niko Naumann
Niko Naumann*
Affiliation:
Mathematisches Institut der WWU Münster Einsteinstr. 62 48149 Münster Germany, e-mail: naumannn@math.uni-muenster.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the interplay between canonical heights and endomorphisms of an abelian variety 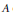$A$ over a number field $k$. In particular we show that whenever the ring of endomorphisms defined over $k$ is strictly larger than 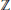$\mathbb{Z}$ there will be 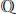$\mathbb{Q}$-linear relations among the values of a canonical height pairing evaluated at a basis modulo torsion of 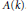$A(k)$.

Keywords

11G1014K15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 2 , 01 June 2004 , pp. 271 - 279
Copyright
Copyright © Canadian Mathematical Society 2004

References

[FLSSSW] Flynn, E., Leprévost, F., Schaefer, E., Stein, W., Stoll, M. and Wetherell, J., Empirical evidence for the Birch and Swinnerton-Dyer conjectures for modular jacobians of genus 2 curves. Math. Comp. (236) 70 (2001), 1675–1697.Google Scholar
[La] Lang, S., Fundamentals of Diophantine Geometry. Springer, New York, 1983.Google Scholar
[Mi2] Milne, J. S., On the Arithmetic of Abelian Varieties. Invent.Math. 17 (1972), 177–190.Google Scholar
[Mu] Mumford, D., Abelian Varieties. Tata Inst. Fund. Res. Stud. Math. 5, Oxford University Press, 1974.Google Scholar
[Ne] Néron, A., Quasi-fonctions et Hauteurs sur les variétés abéliennes. Ann. of Math. 82 (1965), 249–331.Google Scholar
[Se] Serre, J.-P., Lectures on the Mordell-Weil Theorem. Aspects Math. E15, Vieweg, Braunschweig, 1989.Google Scholar
[Ta] Talamanca, V., A note on height pairings on polarized abelian varieties. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 10 (1999), 57–60.Google Scholar