Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T21:25:46.857Z Has data issue: false hasContentIssue false
  • English
  • Français

A Locally Compact Non Divisible Abelian Group Whose Character Group Is Torsion Free and Divisible

Published online by Cambridge University Press:  20 November 2018

Daniel V. Tausk
Daniel V. Tausk*
Affiliation:
Departamento de Matemática, Universidade de São Paulo, Brazil e-mail: tausk@ime.usp.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It was claimed by Halmos in 1944 that if 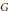$G$ is a Hausdorff locally compact topological abelian group and if the character group of 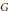$G$ is torsion free, then 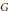$G$ is divisible. We prove that such a claim is false by presenting a family of counterexamples. While other counterexamples are known, we also present a family of stronger counterexamples, showing that even if one assumes that the character group of 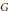$G$ is both torsion free and divisible, it does not follow that 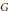$G$ is divisible.

Keywords

22B05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 1 , 01 March 2013 , pp. 213 - 217
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Armacost, D. L., The Structure of Locally Compact Abelian Groups. Monographs and Textbooks in Pure and Applied Mathematics 68. Marcel Dekker, 1981.Google Scholar
[2] Clark, B., Dooley, M., and Schneider, V., Extending topologies from subgroups to groups. Topology Proc. 10 (1985), no. 2, 251–257.Google Scholar
[3] Clark, B. and Schneider, V., The extending topologies. Internat. J. Math. Math. Sci. 7 (1984), no. 3, 621–623. http://dx.doi.org/10.1155/S0161171284000673 Google Scholar
[4] Clark, B. and Schneider, V., The normal extensions of subgroup topologiesProc. Amer. Math. Soc. 97 (1986), no. 1, 163–166. http://dx.doi.org/10.1090/S0002-9939-1986-0831407-9 Google Scholar
[5] Halmos, P. R., Comment on the real lineBull. Amer. Math. Soc. 50 (1944), 877–878. http://dx.doi.org/10.1090/S0002-9904-1944-08255-4 Google Scholar
[6] Harrison, D. K., Infinite abelian groups and homological methods. Ann. of Math. 69 (1959), 366–391. http://dx.doi.org/10.2307/1970188 Google Scholar
[7] Morris, S. A., Pontryagin duality and the structure of locally compact abelian groups. London Mathematical Society Lecture Note Series 29. Cambridge University Press, Cambridge, 1977.Google Scholar