Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T12:19:26.229Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrix Transformations Based on Dirichlet Convolution

Published online by Cambridge University Press:  20 November 2018

Chikkanna Selvaraj  and
Suguna Selvaraj
Chikkanna Selvaraj
Affiliation:
Penn State University—Shenango Campus, 147, Shenango Avenue, Sharon, Pennsylvania 16146, U.S.A., e-mail: ulf@psuvm.psu.edu
Suguna Selvaraj
Affiliation:
Penn State University—Shenango Campus, 147, Shenango Avenue, Sharon, Pennsylvania 16146, U.S.A., e-mail: sxs32@psuvm.psu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is a study of summability methods that are based on Dirichlet convolution. If f(n) is a function on positive integers and x is a sequence such that 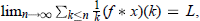then x is said to be Af-summable to L. The necessary and sufficient condition for the matrix Af to preserve bounded variation of sequences is established. Also, the matrix Af is investigated as ℓ − ℓ and G − G mappings. The strength of the Af-matrix is also discussed.

Keywords

11A2540A0540C0540D05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 40 , Issue 4 , 01 December 1997 , pp. 498 - 508
Copyright
Copyright © Canadian Mathematical Society 1997

References

1. Chandrasekharan, K., Arithmetical functions. Chapter I, Springer-Verlag, New York, 1970.Google Scholar
2. Fricke, G. H. and Fridy, J. A., Matrix summability of geometrically dominated series. Canad. J. Math. (3) 39 (1987), 568–582.Google Scholar
3. Fridy, J. A., Divisor summability methods. J. Math. Anal. Appl. (2) 12 (1965), 235–243.Google Scholar
4. Knopp, K. and Lorentz, G. G., Beiträge zur absoluten limitierung. Arch.Math. 2 (1949), 10–16.Google Scholar
5. Mears, F. M., Absolute regularity and the Nörlund mean. Ann. of Math. (3) 38 (1937), 594–601.Google Scholar
6. Rubel, L. A., An abelian theorem for number-theoretic sums. Acta Arith. 6 (1960), 175–177; Correction, Acta Arith. 6 (1961), 523.Google Scholar
7. Segal, S. L., Dirichlet convolutions and the Silverman-Toeplitz conditions, Acta Arith. X (1964), 287–291.Google Scholar
8. Segal, S. L., A note on Dirichlet convolutions, Canad. Math. Bull. (4) 9 (1966), 457–462.Google Scholar