No CrossRef data available.
Article contents
Mean value of real Dirichlet characters using a double Dirichlet series
Published online by Cambridge University Press: 22 March 2023
Abstract
We study the double character sum 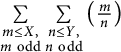 $\sum \limits _{\substack {m\leq X,\\m\mathrm {\ odd}}}\sum \limits _{\substack {n\leq Y,\\n\mathrm {\ odd}}}\left (\frac {m}{n}\right )$ and its smoothly weighted counterpart. An asymptotic formula with power saving error term was obtained by Conrey, Farmer, and Soundararajan by applying the Poisson summation formula. The result is interesting because the main term involves a non-smooth function. In this paper, we apply the inverse Mellin transform twice and study the resulting double integral that involves a double Dirichlet series. This method has two advantages—it leads to a better error term, and the surprising main term naturally arises from three residues of the double Dirichlet series.
$\sum \limits _{\substack {m\leq X,\\m\mathrm {\ odd}}}\sum \limits _{\substack {n\leq Y,\\n\mathrm {\ odd}}}\left (\frac {m}{n}\right )$ and its smoothly weighted counterpart. An asymptotic formula with power saving error term was obtained by Conrey, Farmer, and Soundararajan by applying the Poisson summation formula. The result is interesting because the main term involves a non-smooth function. In this paper, we apply the inverse Mellin transform twice and study the resulting double integral that involves a double Dirichlet series. This method has two advantages—it leads to a better error term, and the surprising main term naturally arises from three residues of the double Dirichlet series.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society



