Article contents
Mean Value Theorem for the m-Integral of Dinculeanu
Published online by Cambridge University Press: 20 November 2018
Extract
The classical mean value theorem asserts that if f is a real, bounded, Riemann integrable function defined on a finite real interval a≤t≤b, then 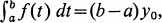 , where infa≤t≤bf(t)≤y0supa≤t≤bf(t). The extensions of Choquet [3], Price [15], and of this paper generalize the fact that y0 belongs to the closure of the convex hull of f([a, b]). The version of Choquet ([3, p. 38]) applies to a continuous function on a compact interval with values in a Banach space; that of Price ([15, p. 24]) applies to a bilinear integral of a special type containing the Birkhoff integral [2]. The m-integral of Dinculeanu [6] (specialization of Bartle's *- integral [1]) leaves intact the Lebesgue dominated convergence theorem and is strong enough to support an extended development. The paper is organized as follows: the object of §2 is to express the integral of a bounded m-integrable function as a limit of Riemann sums; §3 gives Price's generalization of "convex hull" [15]; the theorem of the paper is established in §4; §5 gives applications to vector differentiation which, for continuously differentiable functions, contain results of Dieudonné [5] and McLeod [13].
, where infa≤t≤bf(t)≤y0supa≤t≤bf(t). The extensions of Choquet [3], Price [15], and of this paper generalize the fact that y0 belongs to the closure of the convex hull of f([a, b]). The version of Choquet ([3, p. 38]) applies to a continuous function on a compact interval with values in a Banach space; that of Price ([15, p. 24]) applies to a bilinear integral of a special type containing the Birkhoff integral [2]. The m-integral of Dinculeanu [6] (specialization of Bartle's *- integral [1]) leaves intact the Lebesgue dominated convergence theorem and is strong enough to support an extended development. The paper is organized as follows: the object of §2 is to express the integral of a bounded m-integrable function as a limit of Riemann sums; §3 gives Price's generalization of "convex hull" [15]; the theorem of the paper is established in §4; §5 gives applications to vector differentiation which, for continuously differentiable functions, contain results of Dieudonné [5] and McLeod [13].
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972
References
- 1
- Cited by


