Hostname: page-component-5cf477f64f-r2nwp Total loading time: 0 Render date: 2025-04-02T11:30:16.924Z Has data issue: false hasContentIssue false
  • English
  • Français

Measure comparison problems for dilations of convex bodies

Part of: Nonlinear functional analysis General convexity Limit theorems

Published online by Cambridge University Press:  08 January 2025

Malak Lafi  and
Artem Zvavitch Open the ORCID record for Artem Zvavitch [Opens in a new window]
Malak Lafi
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH, 44242 e-mail: mlafi1@kent.edu
Artem Zvavitch*
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH, 44242 e-mail: mlafi1@kent.edu
*
e-mail: azvavitc@kent.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a version of the Busemann-Petty problem for 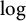$\log $-concave measures with an additional assumption on the dilates of convex, symmetric bodies. One of our main tools is an analog of the classical large deviation principle applied to 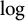$\log $-concave measures, depending on the norm of a convex body. We hope this will be of independent interest.

Keywords

Busemann-Petty problemlog-concavitylarge deviation

MSC classification

Primary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 52A21: Finite-dimensional Banach spaces (including special norms, zonoids, etc.)
Secondary: 46T12: Measure (Gaussian, cylindrical, etc.) and integrals (Feynman, path, Fresnel, etc.) on manifolds 60F10: Large deviations
Type
Article
Information
Canadian Mathematical Bulletin , Volume 68 , Issue 1 , March 2025 , pp. 270 - 285
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Both authors are supported in part by the U.S. National Science Foundation Grant DMS-1101636 and the United States - Israel Binational Science Foundation (BSF) Grant 2018115.

References

Bobkov, S. G. and Nazarov, F., Sharp dilation-type inequalities with fixed parameter of convexity. Zap. Nauchn. Sem. POMI 351(2007), 54–78. English translation in J. Math. Sci. (N.Y.) 152(2008), 826–839.CrossRefGoogle Scholar
Bogachev, V., Gaussian measures, Mathematical Surveys and Monographs, Vol. 62, American Mathematical Society, Providence, RI, 1998.CrossRefGoogle Scholar
Borell, C., Convex set functions in d-space . Period. Math. Hungar 6(1975), no. 2, 111–136.CrossRefGoogle Scholar
Bourgain, J., On the Busemann-Petty problem for perturbations of the ball . Geom. Funct. Anal. 1(1991), 1–13.CrossRefGoogle Scholar
Busemann, H. and Petty, C. M., Problems on convex bodies . Math. Scand. 4(1956), 88–94.CrossRefGoogle Scholar
Cordero-Erausquin, D., Fradelizi, M. and Maurey, B., The (B) conjecture for the Gaussian measure of dilates of symmetric convex sets and related problems . J. Funct. Anal. 214(2004), no. 2, 410–427.CrossRefGoogle Scholar
Gardner, R. J., Intersection bodies and the Busemann-Petty problem . Trans. Amer. Math. Soc. 342(1994), no. 1, 435–445.CrossRefGoogle Scholar
Gardner, R. J., Geometric tomography, second edition, Cambridge University Press, New York, 2006.CrossRefGoogle Scholar
Gardner, R. J., The Brunn–Minkowski inequality. Bull. Amer. Math. Soc. (N.S.). 39(2002) no. 3, 355–405.CrossRefGoogle Scholar
Gardner, R. J., Koldobsky, A. and Schlumprecht, Th., An analytic solution to the Busemann-Petty problem on sections of convex bodies . Ann. of Math. (2) 149(1999), no. 2, 691–703.CrossRefGoogle Scholar
Giannopoulos, A., A note on a problem of H. Busemann and C. M. Petty concerning sections of symmetric convex bodies . Mathematika 37(1990), no. 2, 239–244.CrossRefGoogle Scholar
Fradelizi, M., Concentration inequalities for s–concave measures of dilations of Borel sets and applications . Electron. J. Probab. 14(2009), no. 71, 2068–2090.CrossRefGoogle Scholar
Koldobsky, A., Intersection bodies, positive definite distributions and the Busemann-Petty problem . Amer. J. Math. 120(1998), no. 4, 827–840.CrossRefGoogle Scholar
Lutwak, E., Intersection bodies and dual mixed volumes . Adv. Math. 71(1988), no. 2, 232–261.CrossRefGoogle Scholar
Latala, R. and Oleszkiewicz, K., Gaussian measures of dilations of convex symmetric sets . Ann. Probab. 27(1999), no. 4, 1922–1938.CrossRefGoogle Scholar
Milman, V., Personal communication, 2007.Google Scholar
Papadimitrakis, M., On the Busemann-Petty problem about convex, centrally symmetric bodies in ${\mathbb{R}}^n$ . Mathematika 39(1992), no. 2, 258–266.CrossRefGoogle Scholar
Prékopa, A., Logarithmic concave measures with application to stochastic programming . Acta Sci. Math. (Szeged) 32(1971), 301–316 Google Scholar
Prékopa, A., On logarithmic concave measures and functions . Acta Sci. Math. (Szeged) 34(1973), 335–343.Google Scholar
Schneider, R., Convex bodies: The Brunn-Minkowski Theory , second expanded edition, Encyclopedia of Mathematics and Its Applications, Vol. 151, Cambridge University Press, Cambridge, 2014.Google Scholar
Zhang, G., A positive solution to the Busemann-Petty problem in ${\mathbb{R}}^4$ . Ann. of Math. (2) 149(1999), no. 2, 535–543.CrossRefGoogle Scholar
Zvavitch, A., Gaussian measure of sections of convex bodies . Adv. Math. 188(2004), no. 1, 124–136.CrossRefGoogle Scholar
Zvavitch, A., The Busemann-Petty problem for arbitrary measures . Math. Ann. 331(2005), no. 4, 867–887.CrossRefGoogle Scholar
Zvavitch, A., Gaussian measure of sections of dilates and translations of convex bodies . Adv. Appl. Math. 41(2008), no. 2, 247–254.CrossRefGoogle Scholar