Published online by Cambridge University Press: 20 November 2018
In this paper, the concept of the classical 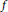 $f$-divergence for a pair of measures is extended to the mixed
$f$-divergence for a pair of measures is extended to the mixed 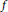 $f$-divergence formultiple pairs ofmeasures. The mixed
$f$-divergence formultiple pairs ofmeasures. The mixed 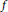 $f$-divergence provides a way to measure the difference between multiple pairs of (probability) measures. Properties for the mixed
$f$-divergence provides a way to measure the difference between multiple pairs of (probability) measures. Properties for the mixed 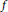 $f$-divergence are established, such as permutation invariance and symmetry in distributions. An Alexandrov–Fenchel type inequality and an isoperimetric inequality for the mixed
$f$-divergence are established, such as permutation invariance and symmetry in distributions. An Alexandrov–Fenchel type inequality and an isoperimetric inequality for the mixed 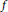 $f$-divergence are proved.
$f$-divergence are proved.