Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T10:02:06.906Z Has data issue: false hasContentIssue false
  • English
  • Français

A Mountain Pass to the Jacobian Conjecture

Published online by Cambridge University Press:  20 November 2018

Marc Chamberland  and
Gary Meisters
Marc Chamberland*
Affiliation:
Dept. of Mathematics and Statistics McMaster University Hamilton, Ontario L8S 4K1 New address: Dept. of Mathematics and Computer Science Grinnell College IA 50112 USA, email: chamberl@math.grin.edu
Gary Meisters
Affiliation:
Dept. of Mathematics and Statistics University of Nebraska-Lincoln NE 68588-0323 USA, email: gmeister@math.unl.edu
*
New address: Dept. of Mathematics and Computer Science Grinnell College IA 50112 USA, email: chamberl@math.grin.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper presents an approach to injectivity theorems via the Mountain Pass Lemma and raises an open question. The main result of this paper (Theorem 1.1) is proved by means of the Mountain Pass Lemma and states that if the eigenvalues of 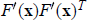${F}'(\text{x}){F}'{{(\text{x})}^{T}}\,$ are uniformly bounded away from zero for 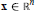$\text{x}\,\in \,{{\mathbb{R}}^{n}}$, where 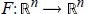$F\,:\,{{\mathbb{R}}^{n}}\,\to \,{{\mathbb{R}}^{n}}$ is a class 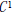${{C}^{1}}$ map, then F is injective. This was discovered in a joint attempt by the authors to prove a stronger result conjectured by the first author: Namely, that a sufficient condition for injectivity of class 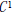${{C}^{1}}$ maps 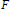$F$ of 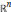${{\mathbb{R}}^{n}}$ into itself is that all the eigenvalues of 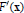${F}'\,(\text{x})$ are bounded away from zero on 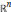${{\mathbb{R}}^{n}}$. This is stated as Conjecture 2.1. If true, it would imply (via Reduction-of-Degree) injectivity of polynomial maps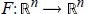$F\,:\,{{\mathbb{R}}^{n}}\,\to \,{{\mathbb{R}}^{n}}$satisfying the hypothesis, 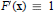$\det F'(x)\equiv 1$, of the celebrated Jacobian Conjecture (JC) of Ott-Heinrich Keller. The paper ends with several examples to illustrate a variety of cases and known counterexamples to some natural questions.

Keywords

14A2514E09InjectivityC1-mapspolynomial mapsJacobian ConjectureMountain Pass
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 4 , 01 December 1998 , pp. 442 - 451
Copyright
Copyright © Canadian Mathematical Society 1998

Footnotes

The first author was partially supported by an NSERC Post-Doctoral Fellowship.

References

1. Ambrosetti, A. and Rabinowitz, P., Dual Variational Methods in Critical Point Theory and Applications. J. Funct. Anal. 14 (1973), 349–381.Google Scholar
2. Bass, H., Connell, E. H. and Wright, D., The Jacobian Conjecture: Reduction of Degree and Formal Expansion of the Inverse. Bull. Amer. Math. Soc. 7 (1982), 287–330.Google Scholar
3. Białynicki-Birula, A. and Rosenlicht, M., Injective morphisms of real algebraic varieties. Proc. Amer. Math. Soc. 13 (1962), 200–203.Google Scholar
4. Brezis, H. and Nirenberg, L., Remarks on Finding Critical Points. Comm. Pure Appl. Math. 44 (1991), 939–963.Google Scholar
5. Campbell, L. A., Rational Samuelson maps are univalent. J. Pure Appl. Algebra 92 (1994), 227–240.Google Scholar
6. Campbell, L. A., Partial Properness and Real Planar Maps. Appl. Math. Lett. (5) 9 (1996), 99–105.Google Scholar
7. Cima, A., van den Essen, A., Gasull, A., Hubbers, E. and Mañosas, F., A polynomial counterexample to the Markus-Yamabe Conjecture on R3. Univ. of Nijmegen, The Netherlands, Mathematics Dept. Report 9551 (Nov. 1995). The final blow to the Markus-Yamabe Conjecture in dimensions n > 2; to appear in Adv. Math.+2;+to+appear+in+Adv.+Math.>Google Scholar
8. van den Essen, A. via Coomes, B. A., Details of Pinchuk's degree (10,25) counterexample to the Strong Real Jacobian Conjecture. Personal communication from Essen via Coomes, June 3, 1994.Google Scholar
9. Deng, Bo, Analytic Conjugation, Global Attractor, and the Jacobian Conjecture. TEX preprint, Spring 1995. Characterizes analytic maps which are globally analytically conjugate to their linear part at a fixed point. See also Rosay and Rudin [29].Google Scholar
10. van den Essen, A., Counterexample to a conjecture of Meisters. Nijmegen Report 9441 (Oct. 1994). The Conjugation Conjecture for F = X − H is false.Google Scholar
11. van den Essen, A. and Hubbers, E., Chaotic Polyomorphisms: Counterexamples to Several Conjectures. Nijmegen Report 9549 (November 1995). Adv. in Appl. Math. (3) 18 (1997), 382–388.Google Scholar
12. van den Essen, A. (ed.), Automorphisms of Affine Spaces. Proceedings of a Conference on Polynomial Automorphisms, at the Princess Beach Resort Casino, Willemstad, Curac¸ao, The Netherlands Antilles, July 4–8, 1994. Kluwer Academic Publishers, 1995.Google Scholar
13. Gale, D. and Nikaidŏ, H., The Jacobian matrix and global univalence. Math. Ann. 159 (1965), 81–93.Google Scholar
14. Gordon, W. B., On the Diffeomorphisms of Euclidean Space. Amer. Math. Monthly 79(1972), 755-759. (See also Addendum (6) 80 (1973), 674–675; and Application (1) 84 (1977), 28–29.)Google Scholar
15. Gorni, G. and Zampieri, G., On cubic-linear polynomial mappings. UDMI/43/96/RR (September 1996), 21 pages, Udine, Italy; Nederl. Akad. Wetensch. Indag. Math., to appear.Google Scholar
16. Keller, O.-H., Ganze Cremona Transformationen. Monatsh Math. 47 (1939), 299–306, Items 6 and 7 in the table on page 301.Google Scholar
17. Meisters, G. H., Jacobian problems in differential equations and algebraic geometry. Rocky Mountain J. Math. 12 (1982), 679–705.Google Scholar
18. Meisters, G. H., Inverting polynomial maps of n-space by solving differential equations. In: Delay and Differential Equations, Proceedings in Honor of George Seifert, Ames, Iowa, October 18–19, 1991 (Eds.: Fink/Miller/Kliemann). World Scientific, Singapore-River Edge, NJ-London-Hong Kong, 1992, 107– 166.Google Scholar
19. Meisters, G. H., Wanted: A Bad Matrix. Amer. Math. Monthly 102 (1995), 546–550 Google Scholar
20. Meisters, G. H., Poly Map Bib 1997, 30 pp. World Wide Web, http://www.math.unl.edu/¾gmeister/.Google Scholar
21. Meisters, G. H., A Biography of the Markus-YamabeConjecture. In: Aspects of Mathematics: Algebra, Geometry and Several Complex Variables. Proc. of Conf. June 10–13, 1996, at HKU, to appear.Google Scholar
22. Noble, and Daniel, , Applied Linear Algebra. 2nd edn, Prentice-Hall, 1977, 431, Theorem 11.7.Google Scholar
23. Palais, R. S. and Smale, S., A generalized Morse Theory. Bull. Amer.Math. Soc. 70 (1964), 165–171.Google Scholar
24. Pinchuk, S. I., Counterexample to the Strong Real Jacobian Conjecture. Math. Zeit. 217 (1994), 1–4.Google Scholar
25. Plastock, R., Homeomorphisms between Banach spaces. Trans. Amer.Math. Soc. 200 (1974), 169–183.Google Scholar
26. Pucci, P. and Serrin, J., The Structure of the Critical Set in the Mountain Pass Theorem. Trans. Amer. Math. Soc. 299 (1987), 115–132.Google Scholar
27. Rabier, P. J., On Global Diffeomorphisms of Euclidean Space. Nonlinear Anal. 21 (1993), 925–947.Google Scholar
28. Rabinowitz, P. H., MinimaxMethods in Critical Point Theory with Applications to Differential Equations. CBMS Regional Conference Series in Mathematics 65. Published for the Conference Board of the Mathematical Sciences,Washington, DC, by the American Mathematical Society, Providence, RI, 1986.Google Scholar
29. Rosay, J.-P. and Rudin, W., Holomorphic maps from Cn to Cn . Trans.Amer.Math. Soc. 310 (1988), 47–86. Compare Theorem in the Appendix with Bo Deng [9].Google Scholar
30. Rudin, W., Injective Polynomial Maps are Automorphisms. Amer. Math. Monthly 102 (1995), 540–543.Google Scholar
31. Smyth, B. and Xavier, F., Injectivity of Local Diffeomorphisms from Nearly Spectral Conditions. J. Differential Equations 130 (1996), 406–414.Google Scholar
32. Wright, D., On the Jacobian Conjecture. Illinois J. Math.25 (1981), 423–440.Google Scholar
33. Yagzhev, A. V., Keller's Problem. Siberian Math. J. 21 (1981), 747–754.Google Scholar