Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T04:06:50.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Multivariate Rankin–Selberg Integrals on GL4 and GU(2, 2)

Published online by Cambridge University Press:  20 November 2018

Aaron Pollack  and
Shrenik Shah
Aaron Pollack
Affiliation:
School of Mathematics, Institute for Advanced Study, Princeton, NJ 08540, USA, e-mail : aaronjp@math.ias.edu
Shrenik Shah
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA, e-mail : snshah@math.columbia.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Inspired by a construction by Bump, Friedberg, and Ginzburg of a two-variable integral representation on 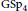$\text{GS}{{\text{p}}_{4}}$ for the product of the standard and spin $L$-functions, we give two similar multivariate integral representations. The first is a three-variable Rankin-Selberg integral for cusp forms on 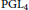$\text{PG}{{\text{L}}_{4}}$ representing the product of the $L$-functions attached to the three fundamental representations of the Langlands $L$-group 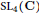$\text{S}{{\text{L}}_{\text{4}}}\left( \text{C} \right)$. The second integral, which is closely related, is a two-variable Rankin-Selberg integral for cusp forms on 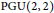$\text{PGU}\left( 2,\,2 \right)$ representing the product of the degree $8$ standard $L$-function and the degree $6$ exterior square $L$-function.

Keywords

11F6611F55automorphic formL-functionRankin–Selbergmethodunitary groupexterior squareLanglands program
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 4 , 01 December 2018 , pp. 822 - 835
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Bump, D. and Friedberg, S., The exterior square automorphic L-functions on GL(«). In: Festschrift in honor of 1.1. Piatetski-Shapiro on the occasion of his sixtieth birthday, Part II (Ramat Aviv, 1989), Israel Math. Conf. Proa, 3, Weizmann, Jerusalem, 1990, pp. 47–65.Google Scholar
[2] Bump, D., Friedberg, S., Ginzburg, D., Rankin-Selberg integrals in two complex variables. Math. Ann. 313 (1999), no. 4, 731-761. http://dx.doi.Org/10.1007/s002080050280Google Scholar
[3] Bump, D., Furusawa, M., and Ginzburg, D., Non-unique models in the Rankin-Selberg method. J. Reine Angew. Math. 468 (1995), 77–111.Google Scholar
[4] Casselman, W. and Shalika, J., The unramified principal series ofp-adic groups. II. The Whittaker function. Compositio Math. 41 (1980), no. 2, 207-231.Google Scholar
[5] Furusawa, M. and Morimoto, K., Shalika periods on GU(2,2). Proc. Amer. Math. Soc. 141 (2013), no. 12,4125-4137. http://dx.doi.org/10.1090/S0002-9939-2013-11690-4Google Scholar
[6] Gan, W. T. and Hundley, J., The spin L-function of quasi-split D4. IMRP Int. Math. Res. Pap. (2006), Art. ID 68213, 74.Google Scholar
[7] Ginzburg, D. and Hundley, J., Multivariable Rankin-Selberg integrals for orthogonal groups. Int. Math. Res. Not. (2004), no. 58, 3097-3119.Google Scholar
[8] Hundley, J., Spin L-functions for GSO10 and GSO12. Israel J. Math. 165 (2008), 103–132. http://dx.doi.Org/10.1007/s11856-008-1006-1Google Scholar
[9] Hundley, J. and Shen, X., A multi-variable Rankin-Selberg integral for a product of GL2-twisted spinor L-functions. Monatsh. Math. 181 (2016), no. 2, 355-403. http://dx.doi.org/10.1007/s00605-015-0868-7Google Scholar
[10] Pollack, A., Unramified Godement-Jacquet theory for the spin similitude group. J. Ramanujan Math. Soc, to appear.Google Scholar
[11] Pollack, A. and Shah, S., The Spin L-function on GSp6 via a non-unique model. Amer. J. Math., to appear.Google Scholar
[12] Pollack, A. and Shah, S., A multivariate integral representation on GL2 x GSp4 inspired by the pullback formula. Trans. Amer. Math. Soc, to appear. http://dx.doi.Org/10.1090/tran/7463Google Scholar
[13] Pollack, A. and Shah, S., On the Rankin-Selberg integral ofKohnen and Skoruppa. Math. Res. Lett. 24 (2017), no. 1, 173-222. http://dx.doi.org/10.4310/MRL.2017.v24.n1.a8Google Scholar
[14] Skinner, C., Galois representations associated with unitary groups over Q. Algebra Number Theory 6 (2012), no. 8, 1697-1717. http://dx.doi.Org/10.2140/ant.2012.6.1697Google Scholar
[15] Tamir, B., On L-functions and intertwining operators for unitary groups. Israel J. Math. 73 (1991), no. 2, 161-188. http://dx.doi.org/10.1007/BF02772947Google Scholar