Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T05:36:25.691Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Formula for the Energy of Bulk Superconductivity

Published online by Cambridge University Press:  20 November 2018

Ayman Kachmar
Ayman Kachmar*
Affiliation:
Department of Mathematics, Lebanese University, Hadat, Lebanon e-mail: ayman.kashmar@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The energy of a type 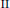$\text{II}$ superconductor submitted to an external magnetic field of intensity close to the second critical field is given by the celebrated Abrikosov energy. If the external magnetic field is comparable to and below the second critical field, the energy is given by a reference function obtained as a special (thermodynamic) limit of a non-linear energy. In this note, we give a new formula for this reference energy. In particular, we obtain it as a special limit of a linear energy defined over configurations normalized in the 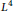${{L}^{4}}$-norm.

Keywords

35B4035P1535Q56Ginzburg–Landau functional
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 553 - 563
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Aftalion, A. and Serfaty, S., Lowest Landau level approach in superconductivity for the Abrikosov lattice close to HC2. Selecta Math. (N.S.) 13(2007), no. 2,183-202. http://dx.doi.org/10.1007/s00029-007-0043-7 Google Scholar
[2] Almog, Y., Non-linear surface superconductivity in three dimensions in the large K limit. Commun. Contemp. Math. 6(2004), no. 4, 637–652. http://dx.doi.org/10.1142/S021 91 9970400146X Google Scholar
[3] Attar, K., The ground state energy of the two dimensional Ginzburg-Landau functional with variable magnetic field. Ann. Inst. H. Poincaré Anal. Non Linéaire 32(2015), no. 2, 325–345. http://dx.doi.org/10.1016/j.anihpc.2013.12.002 Google Scholar
[4] Attar, K., Energy and vorticity of the Ginzburg-Landau model with variable magnetic field. Asymptot.Anal. 93(2015), no. 1-2, 75–114. http://dx.doi.org/10.3233/ASY-151286 Google Scholar
[5] Attar, K., Pinning with a variable magnetic field of the two dimensional Ginzburg-Landau model. Nonlinear Anal., to appear.arxiv:1503.06500Google Scholar
[6] de Gennes, P. G., Superconductivity of metals and alloys. Benjamin, New York, 1966.Google Scholar
[7] Fournais, S. and Helffer, B.. Spectral methods in surface superconductivity.Progress in Nonlinear Differential Equations and Their Applications, 77, Birkhauser Boston, Boston, MA, 2010.Google Scholar
[8] Fournais, S. and Helffer, B., Bulk superconductivity in Type II superconductors near the second critical field. J. Eur. Math. Soc. 12(2010), no. 2, 461–470. http://dx.doi.org/1 0.41 71/JEMS/205 Google Scholar
[9] Fournais, S. and Kachmar, A., The ground state energy of the three dimensional Ginzburg-Landau functional. Parti.Bulk regime.Communications in Partial Differential Equations 38(2013), 339–383. http://dx.doi.org/10.1080/03605302.2012.71 7156 Google Scholar
[10] Fournais, S. and Kachmar, A., Nucleation of bulk superconductivity close to critical magnetic field. Adv. Math. 226(2011), no. 2, 1213–1258. http://dx.doi.org/10.101 6/j.aim.2O10.08.004 Google Scholar
[11] Fournais, S., Kachmar, A., and Persson, M., The ground state energy of the three dimensional Ginzburg-Landau functional. Part II. Surface regime.J. Math. Pures Appl. 99(2013), no. 3, 343–374. http://dx.doi.org/10.101 6/j.matpur.2O12.09.002 Google Scholar
[12] Fournais, S. and Raymond, N., Optimal magnetic Sobolev constants in the semi-classical limit.To appear, Annales de l'Institut Henri Poincaré Anal. Non-Linéaire. arxiv:1411.5554v1Google Scholar
[13] Kachmar, A., The Ginzburg-Landau order parameter near the second critical field. SIAM. J. Math. Anal 46(2014), no. 1, 572–587. http://dx.doi.org/10.1137/130935963 Google Scholar
[14] Sandier, E. and Serfaty, S., Vortices in the magnetic Ginzburg-Landau model.Progress in Nonlinear Differential Equations and Their Applications, 70, Birkhauser, Boston, 2007.Google Scholar
[15] Sandier, E. and Serfaty, S., The decrease of bulk superconductivity close to the second critical field in the Ginzburg-Landau model.SIAM. J. Math. Anal. 34(2003), no. 4, 939–956. http://dx.doi.org/10.1137/S0036141002406084 Google Scholar