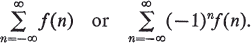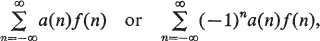Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Krishnaiah, P. V.
and
Rao, R. Sita Rama Chandra
1979.
On Berndt's Method in Arithmetical Functions and Contour Integration.
Canadian Mathematical Bulletin,
Vol. 22,
Issue. 2,
p.
177.
Sitaramachandrarao, R
and
Krishnaiah, P.V
1986.
On the sums Σn ⩽ x A(f(n)) and Σp ⩽ x A(f(p)).
Journal of Number Theory,
Vol. 23,
Issue. 2,
p.
149.
Balakrishnan, U
and
Pétermann, Y.-F.S
1998.
Asymptotic Estimates for a Class of Summatory Functions.
Journal of Number Theory,
Vol. 70,
Issue. 1,
p.
1.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
179.
Alkan, Emre
2011.
On Dirichlet L-functions with periodic coefficients and Eisenstein series.
Monatshefte für Mathematik,
Vol. 163,
Issue. 3,
p.
249.