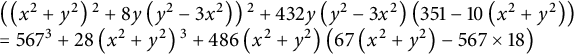1 Introduction
A disk has the property that it can be rotated between two fixed parallel lines without losing contact with either line. It has been known for a long time that there are many other plane convex bodies with the same property. Such plane convex bodies are called plane convex bodies “of constant width” or “orbiforms.” Their boundaries are of course called “plane convex curves of constant width.” A classical noncircular example is the Reuleaux triangle [6], which is made of three circular arcs. But a noncircular plane convex curve of constant width can be smooth, and not having any circular arc in its boundary. The notion of a convex body of constant width can of course be extended to higher dimensions. For a recent book on the topic, we refer the reader to [Reference Martinez-Maure4].
In this paper, we are essentially interested in noncircular algebraic curves of constant width. Rabinowitz [Reference Rabinowitz5] found that the zero set of the following polynomial
![]() $P\in \mathbb {R}\left [ X,Y\right ] $
forms a noncircular algebraic curve of constant width in
$P\in \mathbb {R}\left [ X,Y\right ] $
forms a noncircular algebraic curve of constant width in
![]() $\mathbb {R}^{2}$
:
$\mathbb {R}^{2}$
:
 $$ \begin{align*} \begin{array} [c]{ll} P\left( x,y\right) &:= \left( x^{2}+y^{2}\right) {}^{4}-45\left( x^{2}+y^{2}\right) {}^{3}-41283\left( x^{2}+y^{2}\right) {}^{2}\\ & \quad +7950960\left( x^{2}+y^{2}\right) +16\left( x^{2} -3y^{2}\right) {}^{3}+48\left( x^{2}+y^{2}\right) \left( x^{2} -3y^{2}\right) {}^{2}\\ & \quad +x\left( x^{2}-3y^{2}\right) \left( 16\left( x^{2} +y^{2}\right) {}^{2}-5544\left( x^{2}+y^{2}\right) +266382\right) -720^{3}\text{.} \end{array} \end{align*} $$
$$ \begin{align*} \begin{array} [c]{ll} P\left( x,y\right) &:= \left( x^{2}+y^{2}\right) {}^{4}-45\left( x^{2}+y^{2}\right) {}^{3}-41283\left( x^{2}+y^{2}\right) {}^{2}\\ & \quad +7950960\left( x^{2}+y^{2}\right) +16\left( x^{2} -3y^{2}\right) {}^{3}+48\left( x^{2}+y^{2}\right) \left( x^{2} -3y^{2}\right) {}^{2}\\ & \quad +x\left( x^{2}-3y^{2}\right) \left( 16\left( x^{2} +y^{2}\right) {}^{2}-5544\left( x^{2}+y^{2}\right) +266382\right) -720^{3}\text{.} \end{array} \end{align*} $$
Then, he raised the following open questions: “The polynomial curve found is pretty complicated. Can it be put in simpler form? Our polynomial is of degree 8. Is there one with lower degree? What is the lowest degree polynomial whose graph is a noncircular curve of constant width?” A couple of years ago, Bardet and Bayen [Reference Bardet and Bayen1, Corollary 2.1] proved that the degree of P, that is
![]() $8$
, is the minimum possible degree for a noncircular plane convex curve of constant width. Here, we emphasize the convexity assumption, because it is implicit in the statement of Corollary 2.1 in [Reference Bardet and Bayen1]. In this short note, we provide additional answers to Rabinowitz’s open questions. First, we recall the notion of a plane hedgehog curve of constant width, and we notice that in this setting, we can find algebraic curves of constant width much simpler. Second, we give an example of a noncircular algebraic curve of constant width whose equation is simpler than the one of Rabinowitz. Finally, we notice that we can deduce from it (relatively) simple examples in higher dimensions.
$8$
, is the minimum possible degree for a noncircular plane convex curve of constant width. Here, we emphasize the convexity assumption, because it is implicit in the statement of Corollary 2.1 in [Reference Bardet and Bayen1]. In this short note, we provide additional answers to Rabinowitz’s open questions. First, we recall the notion of a plane hedgehog curve of constant width, and we notice that in this setting, we can find algebraic curves of constant width much simpler. Second, we give an example of a noncircular algebraic curve of constant width whose equation is simpler than the one of Rabinowitz. Finally, we notice that we can deduce from it (relatively) simple examples in higher dimensions.
2 Plane algebraic hedgehogs of constant width
Here, we will follow more or less [Reference Martini, Montejano and Oliveros2].
Definition For any smooth function
![]() $h:\mathbb {\,S} $
$h:\mathbb {\,S} $
![]() $^{1}=\mathbb {R}\setminus 2\pi \mathbb {Z}\rightarrow \mathbb {R} ,\theta \mapsto h\left ( \theta \right ) $
, we let
$^{1}=\mathbb {R}\setminus 2\pi \mathbb {Z}\rightarrow \mathbb {R} ,\theta \mapsto h\left ( \theta \right ) $
, we let
![]() $\mathcal {H}_{h}$
denote the envelope of the family of lines given by
$\mathcal {H}_{h}$
denote the envelope of the family of lines given by
where
![]() $\left ( x,y\right ) $
are the coordinates in the canonical basis of the Euclidean vector plane
$\left ( x,y\right ) $
are the coordinates in the canonical basis of the Euclidean vector plane
![]() $\mathbb {R}^{2}$
. We say that
$\mathbb {R}^{2}$
. We say that
![]() $\mathcal {H}_{h}$
is the plane hedgehog with support function
$\mathcal {H}_{h}$
is the plane hedgehog with support function
![]() $h$
, and that
$h$
, and that
![]() $\mathcal {H}_{h}$
is projective if
$\mathcal {H}_{h}$
is projective if
![]() $h(\theta +\pi )=-h(\theta )$
for all
$h(\theta +\pi )=-h(\theta )$
for all
![]() $\theta \in \mathbb {S}^{1}$
.
$\theta \in \mathbb {S}^{1}$
.
Partial differentiation of 1 yields
From 1 and 2, the parametric equations for
![]() $\mathcal {H}_{h}$
are
$\mathcal {H}_{h}$
are
 $$ \begin{align*} \left\{ \begin{array} [c]{r} x=h(\theta)\cos\theta-h^{\prime}(\theta)\sin\theta,\\ y=h(\theta)\sin\theta+h^{\prime}(\theta)\cos\theta\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array} [c]{r} x=h(\theta)\cos\theta-h^{\prime}(\theta)\sin\theta,\\ y=h(\theta)\sin\theta+h^{\prime}(\theta)\cos\theta\text{.} \end{array} \right. \end{align*} $$
The family of lines
![]() $\left ( D\left ( \theta \right ) \right ) {}_{\theta \in \mathbb {S}^{1}}$
of which
$\left ( D\left ( \theta \right ) \right ) {}_{\theta \in \mathbb {S}^{1}}$
of which
![]() $\mathcal {H}_{h}$
is the envelope is the family of “support lines” of
$\mathcal {H}_{h}$
is the envelope is the family of “support lines” of
![]() $\mathcal {H}_{h}$
. Suppose that
$\mathcal {H}_{h}$
. Suppose that
![]() $\mathcal {H}_{h}$
has a well-defined tangent line at the point
$\mathcal {H}_{h}$
has a well-defined tangent line at the point
![]() $(x,y)$
, say T. Then, T is the support line with equation 1: the unit vector
$(x,y)$
, say T. Then, T is the support line with equation 1: the unit vector
![]() $u(\theta )=(\cos \theta ,\sin \theta )$
is normal to T and
$u(\theta )=(\cos \theta ,\sin \theta )$
is normal to T and
![]() $h(\theta )$
may be interpreted as the signed distance from the origin to T.
$h(\theta )$
may be interpreted as the signed distance from the origin to T.
A plane hedgehog is thus simply a plane envelope that has exactly one oriented support line in each direction. A singularity-free plane hedgehog is simply a convex curve. A plane hedgehog is projective if it has exactly one nonoriented support line in each direction.
Now, we can define the width, say
![]() $w_{h}\left ( \theta \right ) $
, of such a plane hedgehog
$w_{h}\left ( \theta \right ) $
, of such a plane hedgehog
![]() $\mathcal {H}_{h}$
in the direction
$\mathcal {H}_{h}$
in the direction
![]() $u\left ( \theta \right ) $
to be the signed distance between the two support lines of
$u\left ( \theta \right ) $
to be the signed distance between the two support lines of
![]() $\mathcal {H}_{h}$
that are orthogonal to
$\mathcal {H}_{h}$
that are orthogonal to
![]() $u\left ( \theta \right ) $
, that is, by
$u\left ( \theta \right ) $
, that is, by
Thus, plane projective hedgehogs are hedgehogs of constant width
![]() $0$
, and the condition that a plane hedgehog
$0$
, and the condition that a plane hedgehog
![]() $\mathcal {H}_{h}$
is of constant width
$\mathcal {H}_{h}$
is of constant width
![]() $2r$
is simply that its support function h has the form
$2r$
is simply that its support function h has the form
![]() $f+r$
, where f is the support function of a projective hedgehog. Here are three examples of plane hedgehogs: (a) a convex hedgehog of constant width; (b) a hedgehog with four cusps; and (c) a plane projective hedgehog which is a hypocycloid with three cusps (Figure 1).
$f+r$
, where f is the support function of a projective hedgehog. Here are three examples of plane hedgehogs: (a) a convex hedgehog of constant width; (b) a hedgehog with four cusps; and (c) a plane projective hedgehog which is a hypocycloid with three cusps (Figure 1).

Figure 1 Three examples of plane hedgehogs.
Theorem The projective hedgehog
![]() $\mathcal {H} {}_{h}\subset \mathbb {R}^{2}$
with support function
$\mathcal {H} {}_{h}\subset \mathbb {R}^{2}$
with support function
![]() $h:\mathbb {S} {}^{1}\rightarrow \mathbb {R}$
,
$h:\mathbb {S} {}^{1}\rightarrow \mathbb {R}$
,
![]() $\theta \mapsto \sin \left ( 3\theta \right ) $
is a noncircular algebraic curve of constant width
$\theta \mapsto \sin \left ( 3\theta \right ) $
is a noncircular algebraic curve of constant width
![]() $0$
with equation
$0$
with equation
Proof. We already know that
![]() $\mathcal {H}_{h}$
is a noncircular curve of constant width
$\mathcal {H}_{h}$
is a noncircular curve of constant width
![]() $0$
. From the parametric equations for
$0$
. From the parametric equations for
![]() $\mathcal {H}_{h}$
, we deduce that
$\mathcal {H}_{h}$
, we deduce that
Now,
![]() $h:\mathbb {S}^{1}\rightarrow \mathbb {R}$
,
$h:\mathbb {S}^{1}\rightarrow \mathbb {R}$
,
![]() $\theta \mapsto \sin \left ( 3\theta \right ) $
is the restriction of the polynomial
$\theta \mapsto \sin \left ( 3\theta \right ) $
is the restriction of the polynomial
![]() $-y\left ( y^{2}-3x^{2}\right ) $
to the unit circle
$-y\left ( y^{2}-3x^{2}\right ) $
to the unit circle
![]() $\mathbb {S}^{1}$
, and the linearization of
$\mathbb {S}^{1}$
, and the linearization of
![]() $-y\left ( y^{2}-3x^{2}\right ) $
as a trigonometric function of
$-y\left ( y^{2}-3x^{2}\right ) $
as a trigonometric function of
![]() $\theta $
gives
$\theta $
gives
From the above two equations, we deduce easily that
▪
3 A noncircular algebraic curve of constant width whose equation is not too complicated
Any hedgehog whose support function
![]() $h:\mathbb {S}^{1}\rightarrow \mathbb {R}$
is of the form
$h:\mathbb {S}^{1}\rightarrow \mathbb {R}$
is of the form
![]() $h\left ( \theta \right ) =r-\sin \left ( 3\theta \right ) $
, for some constant r, is a hedgehog of constant width
$h\left ( \theta \right ) =r-\sin \left ( 3\theta \right ) $
, for some constant r, is a hedgehog of constant width
![]() $2r$
. Such a function
$2r$
. Such a function
![]() $h:\mathbb {S}^{1}\rightarrow \mathbb {R}$
is the support function of a convex body if and only if
$h:\mathbb {S}^{1}\rightarrow \mathbb {R}$
is the support function of a convex body if and only if
![]() $\left ( h+h^{\prime \prime }\right ) \left ( \theta \right ) =r-8\sin \left ( 3\theta \right ) \geq 0$
, for all
$\left ( h+h^{\prime \prime }\right ) \left ( \theta \right ) =r-8\sin \left ( 3\theta \right ) \geq 0$
, for all
![]() $\theta \in \mathbb {S}^{1}$
, that is, if and only if
$\theta \in \mathbb {S}^{1}$
, that is, if and only if
![]() $r\geq 8$
. We choose
$r\geq 8$
. We choose
![]() $r=8$
in order to be “as closed as possible” to the previous example.
$r=8$
in order to be “as closed as possible” to the previous example.
Theorem The plane hedgehog
![]() $\mathcal {H}_{h}$
with support function
$\mathcal {H}_{h}$
with support function
![]() $h:\mathbb {S}^{1}\rightarrow \mathbb {R}$
,
$h:\mathbb {S}^{1}\rightarrow \mathbb {R}$
,
![]() $\theta \mapsto 8-\sin \left ( 3\theta \right ) =4\sin ^{3}\theta -3\sin \theta +8$
is a noncircular convex algebraic curve of constant width
$\theta \mapsto 8-\sin \left ( 3\theta \right ) =4\sin ^{3}\theta -3\sin \theta +8$
is a noncircular convex algebraic curve of constant width
![]() $16$
with equation (Figure 2)
$16$
with equation (Figure 2)
 $$ \begin{align} \begin{array} [c]{l} \left( \left( x^{2}+y^{2}\right) {}^{2}+8y\left( y^{2}-3x^{2}\right) \right) {}^{2}+432y\left( y^{2}-3x^{2}\right) \left( 351-10\left( x^{2}+y^{2}\right) \right) \\ \kern12pt=567^{3}+28\left( x^{2}+y^{2}\right) {}^{3}+486\left( x^{2}+y^{2}\right) \left( 67\left( x^{2}+y^{2}\right) -567\times18\right). \end{array} \end{align} $$
$$ \begin{align} \begin{array} [c]{l} \left( \left( x^{2}+y^{2}\right) {}^{2}+8y\left( y^{2}-3x^{2}\right) \right) {}^{2}+432y\left( y^{2}-3x^{2}\right) \left( 351-10\left( x^{2}+y^{2}\right) \right) \\ \kern12pt=567^{3}+28\left( x^{2}+y^{2}\right) {}^{3}+486\left( x^{2}+y^{2}\right) \left( 67\left( x^{2}+y^{2}\right) -567\times18\right). \end{array} \end{align} $$

Figure 2 The noncircular convex curve of constant width
![]() $16$
with equation
$16$
with equation
![]() $(3)$
.
$(3)$
.
Proof. The parametric equations for
![]() $\mathcal {H}_{h}$
are equivalent to:
$\mathcal {H}_{h}$
are equivalent to:
 $$ \begin{align*} \left\{ \begin{array} [c]{l} x=-8\left( \sin^{3}\left( \theta\right) -1\right) \cos\left( \theta\right), \qquad\qquad\\ y=-2\cos\left( 2\theta\right) -\cos\left( 4\theta\right) +8\sin\left( \theta\right) \text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array} [c]{l} x=-8\left( \sin^{3}\left( \theta\right) -1\right) \cos\left( \theta\right), \qquad\qquad\\ y=-2\cos\left( 2\theta\right) -\cos\left( 4\theta\right) +8\sin\left( \theta\right) \text{.} \end{array} \right. \end{align*} $$
Expanding x and y in terms of
![]() $c=\cos \theta $
and
$c=\cos \theta $
and
![]() $s=\sin \theta $
, we obtain after simplification:
$s=\sin \theta $
, we obtain after simplification:
 $$ \begin{align*} \left\{ \begin{array} [c]{l} x=-8\left( s^{3}-1\right) c,\qquad\qquad\\ y=-3+4s\left( 2+3s-2s^{3}\right) \text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array} [c]{l} x=-8\left( s^{3}-1\right) c,\qquad\qquad\\ y=-3+4s\left( 2+3s-2s^{3}\right) \text{.} \end{array} \right. \end{align*} $$
Squaring the first equation and substituting in
![]() $c^{2}=1-s^{2}$
gives us the following system of equations in the three unknowns x, y, and s:
$c^{2}=1-s^{2}$
gives us the following system of equations in the three unknowns x, y, and s:
 $$ \begin{align*} \left\{ \begin{array} [c]{l} 64\left( 1-s^{2}\right) \left( s^{3}-1\right) {}^{2}-x^{2}=0,\quad\\ -3+4s\left( 2+3s-2s^{3}\right) -y=0\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array} [c]{l} 64\left( 1-s^{2}\right) \left( s^{3}-1\right) {}^{2}-x^{2}=0,\quad\\ -3+4s\left( 2+3s-2s^{3}\right) -y=0\text{.} \end{array} \right. \end{align*} $$
We then eliminate s by computing the resultant of the polynomials
![]() $A\left ( s\right ) =64\left ( 1-s^{2}\right ) \left ( s^{3}-1\right ) {}^{2}-x^{2}$
and
$A\left ( s\right ) =64\left ( 1-s^{2}\right ) \left ( s^{3}-1\right ) {}^{2}-x^{2}$
and
![]() $B\left ( s\right ) =-3+4s\left ( 2+3s-2s^{3}\right ) -y$
with Mathematica, and find after simplification that:
$B\left ( s\right ) =-3+4s\left ( 2+3s-2s^{3}\right ) -y$
with Mathematica, and find after simplification that:
 $$ \begin{align*} \begin{array} [c]{l} \left( \left( x^{2}+y^{2}\right) {}^{2}+8y\left( y^{2}-3x^{2}\right) \right) {}^{2}+432y\left( y^{2}-3x^{2}\right) \left( 351-10\left( x^{2}+y^{2}\right) \right) \\ \kern12pt=567^{3}+28\left( x^{2}+y^{2}\right) {}^{3}+486\left( x^{2}+y^{2}\right) \left( 67\left( x^{2}+y^{2}\right) -567\times18\right). \end{array}\\[-34pt] \end{align*} $$
$$ \begin{align*} \begin{array} [c]{l} \left( \left( x^{2}+y^{2}\right) {}^{2}+8y\left( y^{2}-3x^{2}\right) \right) {}^{2}+432y\left( y^{2}-3x^{2}\right) \left( 351-10\left( x^{2}+y^{2}\right) \right) \\ \kern12pt=567^{3}+28\left( x^{2}+y^{2}\right) {}^{3}+486\left( x^{2}+y^{2}\right) \left( 67\left( x^{2}+y^{2}\right) -567\times18\right). \end{array}\\[-34pt] \end{align*} $$
▪
4 Higher dimension
The notion of a hedgehog of constant width can of course be extended to higher dimensions (see, e.g., [Reference Martinez-Maure3]). Each of the above two examples of algebraic curves of constant width admits an axis of symmetry in
![]() $\mathbb {R}^{2}$
. By rotating it around such an axis, we deduce immediately an example of algebraic surface of revolution that is of constant width in
$\mathbb {R}^{2}$
. By rotating it around such an axis, we deduce immediately an example of algebraic surface of revolution that is of constant width in
![]() $\mathbb {R}^{3}$
. More precisely, the algebraic surface with equation
$\mathbb {R}^{3}$
. More precisely, the algebraic surface with equation
![]() $.$
$.$
is a “projective hedgehog” of revolution and a surface of constant width
![]() $0$
in
$0$
in
![]() $\mathbb {R}^{3}$
(see Figure 3, left), and the algebraic surface with equation
$\mathbb {R}^{3}$
(see Figure 3, left), and the algebraic surface with equation
 $$ \begin{align*} \begin{array} [c]{c} \left( \left( x^{2}+y^{2}+z^{2}\right) {}^{2}+8z\left( z^{2}-3\left( x^{2}+y^{2}\right) \right) \right) {}^{2}\\ +432z\left( z^{2}-3\left( x^{2}+y^{2}\right) \right) \left( 351-10\left( x^{2}+y^{2}+z^{2}\right) \right) \\ =567^{3}+28\left( x^{2}+y^{2}+z^{2}\right) {}^{3}\\ +486\left( x^{2}+y^{2}+z^{2}\right) \left( 67\left( x^{2}+y^{2} +z^{2}\right) -567\times18\right) \end{array} \end{align*} $$
$$ \begin{align*} \begin{array} [c]{c} \left( \left( x^{2}+y^{2}+z^{2}\right) {}^{2}+8z\left( z^{2}-3\left( x^{2}+y^{2}\right) \right) \right) {}^{2}\\ +432z\left( z^{2}-3\left( x^{2}+y^{2}\right) \right) \left( 351-10\left( x^{2}+y^{2}+z^{2}\right) \right) \\ =567^{3}+28\left( x^{2}+y^{2}+z^{2}\right) {}^{3}\\ +486\left( x^{2}+y^{2}+z^{2}\right) \left( 67\left( x^{2}+y^{2} +z^{2}\right) -567\times18\right) \end{array} \end{align*} $$
is a convex surface of constant width
![]() $16$
in
$16$
in
![]() $\mathbb {R}^{3}$
(see Figure 3, right).
$\mathbb {R}^{3}$
(see Figure 3, right).

Figure 3 Our two algebraic surfaces of constant width.
There are several methods to explicitly find algebraic constant width bodies, even without being of revolution (see, e.g., [Reference Martinez-Maure4, Section 8.5]).