No CrossRef data available.
Article contents
Nonconstant Continuous Functions whose Tangential Derivative Vanishes along a Smooth Curve
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We provide a simple example showing that the tangential derivative of a continuous function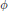 
$\phi $ can vanish everywhere along a curve while the variation of 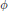$\phi $ along this curve is nonzero. We give additional regularity conditions on the curve and/or the function that prevent this from happening.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
[1] De Pauw, T., Moonens, L., and Pfeffer, W. F., Charges in middle dimensions. J. Math. Pures Appl. (9)
92(2009), no. 1, 86–112.Google Scholar
[2] Federer, H., Geometric measure theory. Die Grundlehren der mathematischen Wissenschaften, 153, Springer-Verlag, New York, 1969.Google Scholar
[3] Pfeffer, W. F., The Riemann approach to integration. Local geometric theory. Cambridge Tracts in Mathematics, 109, Cambridge University Press, Cambridge, 1993.Google Scholar
[5] Whitney, H., A function not constant on a connected set of critical points. Duke Math. J.
1(1935), no. 4, 514–517. doi:10.1215/S0012-7094-35-00138-7Google Scholar
You have
Access