Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T08:37:29.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-spectral Problem for Some Self-similar Measures

Part of: Normed linear spaces and Banach spaces; Banach lattices Nontrigonometric harmonic analysis Classical measure theory

Published online by Cambridge University Press:  28 August 2019

Ye Wang ,
Xin-Han Dong  and
Yue-Ping Jiang
Ye Wang
Affiliation:
College of Mathematics and Econometrics, Hunan University, Changsha, Hunan 410082, P.R. China Department of Mathematics, The University of Iowa, Iowa City, IA 52242, USA Email: hnsdwangye@163.com
Xin-Han Dong
Affiliation:
College of Mathematics and Econometrics, Hunan University, Changsha, Hunan 410082, P.R. China Email: xhdonghnsd@163.comypjiang731@163.com
Yue-Ping Jiang
Affiliation:
College of Mathematics and Econometrics, Hunan University, Changsha, Hunan 410082, P.R. China Email: xhdonghnsd@163.comypjiang731@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that 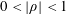$0<|\unicode[STIX]{x1D70C}|<1$ and 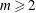$m\geqslant 2$ is an integer. Let 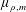$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m}$ be the self-similar measure defined by 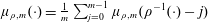$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m}(\cdot )=\frac{1}{m}\sum _{j=0}^{m-1}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m}(\unicode[STIX]{x1D70C}^{-1}(\cdot )-j)$. Assume that 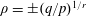$\unicode[STIX]{x1D70C}=\pm (q/p)^{1/r}$ for some 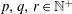$p,q,r\in \mathbb{N}^{+}$ with 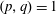$(p,q)=1$ and 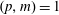$(p,m)=1$. We prove that if 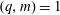$(q,m)=1$, then there are at most $m$ mutually orthogonal exponential functions in 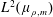$L^{2}(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m})$ and $m$ is the best possible. If 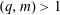$(q,m)>1$, then there are any number of orthogonal exponential functions in 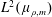$L^{2}(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m})$.

Keywords

self-similar measurespectral measureorthogonal exponential functionFourier transform

MSC classification

Primary: 28A80: Fractals
Secondary: 42C05: Orthogonal functions and polynomials, general theory 46C05: Hilbert and pre-Hilbert spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 2 , June 2020 , pp. 318 - 327
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research is supported in part by the NNSF of China (No. 11831007, No.11571099).

References

Dai, X. R., When does a Bernoulli convolution admit a spectrum? Adv. Math. 231(2012), 1681–1693. https://doi.org/10.1016/j.aim.2012.06.026Google Scholar
Dai, X. R., He, X. G., and Lau, K. S., On spectral N-Bernoulli measures. Adv. Math. 259(2014), 511–531. https://doi.org/10.1016/j.aim.2014.03.026Google Scholar
Dai, X. R. and Sun, Q. Y., Spectral measures with arbitrary Hausdorff dimensions. J. Funct. Anal. 268(2015), 2464–2477. https://doi.org/10.1016/j.jfa.2015.01.005Google Scholar
Deng, Q. R., Spectrality of one dimensional self-similar measures with consecutive digits. J. Math. Anal. Appl. 409(2014), 331–346. https://doi.org/10.1016/j.jmaa.2013.07.046Google Scholar
Dutkay, D., Emami, S., and Lai, C. K., Existence and exactness of exponential Riesz sequences and frames for fractal measures. arxiv:1809.06541Google Scholar
Dutkay, D., Han, D., and Sun, Q. Y., On the spectra of a Cantor measure. Adv. Math. 221(2009), 251–276. https://doi.org/10.1016/j.aim.2008.12.007Google Scholar
Hu, T. Y. and Lau, K. S., Spectral property of the Bernoulli convolutions. Adv. Math. 219(2008), 554–567. https://doi.org/10.1016/j.aim.2008.05.004Google Scholar
Jorgensen, P. and Pedersen, S., Dense analytic subspaces in fractal L 2-spaces. J. Anal. Math. 75(1998), 185–228. https://doi.org/10.1007/BF02788699Google Scholar
Karpilovsky, G., Topics in field theory. North-Holland Publishing Co., Amsterdam, 1989.Google Scholar
Ke, Z. and Sun, Q., Lectures of the theory of numbers. Higher Education Press, Beijing, 2003.Google Scholar
Łaba, I. and Wang, Y., On spectral Cantor measures. J. Funct. Anal. 193(2002), 409–420. https://doi.org/10.1006/jfan.2001.3941Google Scholar
Lai, C. K. and Wang, Y., Non-spectral fractal measures with fourier frames. J. Fractal Geom. 4(2017), 305–327. https://doi.org/10.4171/JFG/52Google Scholar
Li, J. L., Spectra of a class of self-affine measures. J. Funct. Anal. 260(2011), 1086–1095. https://doi.org/10.1016/j.jfa.2010.12.001Google Scholar
Liu, J. C., Dong, X. H., and Li, J. L., Non-spectral problem for the planar self-affine measures. J. Funct. Anal. 273(2017), 705–720. https://doi.org/10.1016/j.jfa.2017.04.003Google Scholar
Strichartz, R., Convergence of Mock Fourier series. J. Anal. Math. 99(2006), 333–353. https://doi.org/10.1007/BF02789451Google Scholar
Solomyak, B., Notes on Bernoulli convolutions. In: Fractal geometry and applications: A Jubilee of Benoît Mandelbrot. Part 1. Proc. Sympos. Pure Math., 72, American Mathematical Society, Providence, RI, 2004, pp. 207–230.10.1090/pspum/072.1/2112107Google Scholar
Wang, Z. Y., Wang, Z. M., Dong, X. H., and Zhang, P. F., Orthogonal exponential functions of self-similar measures with consecutive digits in ℝ. J. Math. Anal. Appl. 467(2018), 1148–1152. https://doi.org/10.1016/j.jmaa.2018.07.062Google Scholar