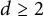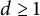1 Introduction
A norm
![]() $\| \cdot \|$
on
$\| \cdot \|$
on
![]() $\mathrm {M}_n$
, the space of
$\mathrm {M}_n$
, the space of
![]() $n\times n$
complex matrices, is unitarily invariant if
$n\times n$
complex matrices, is unitarily invariant if
![]() $\| UAV \|=\| A \|$
for all
$\| UAV \|=\| A \|$
for all
![]() $A\in \mathrm {M}_n$
and unitary
$A\in \mathrm {M}_n$
and unitary
![]() $U,V \in \mathrm {M}_n$
. A norm on
$U,V \in \mathrm {M}_n$
. A norm on
![]() $\mathbb {R}^n$
which is invariant under entrywise sign changes and permutations is a symmetric gauge function. A theorem of von Neumann asserts that any unitarily invariant norm on
$\mathbb {R}^n$
which is invariant under entrywise sign changes and permutations is a symmetric gauge function. A theorem of von Neumann asserts that any unitarily invariant norm on
![]() $\mathrm {M}_n$
is a symmetric gauge function applied to the singular values [Reference Horn and Johnson10, Theorem 7.4.7.2]. For example, the Schatten norms are unitarily invariant and defined for
$\mathrm {M}_n$
is a symmetric gauge function applied to the singular values [Reference Horn and Johnson10, Theorem 7.4.7.2]. For example, the Schatten norms are unitarily invariant and defined for
![]() $d\geq 1$
by
$d\geq 1$
by
in which
![]() $\sigma _1 \geq \sigma _2 \geq \cdots \geq \sigma _n \geq 0$
are the singular values of
$\sigma _1 \geq \sigma _2 \geq \cdots \geq \sigma _n \geq 0$
are the singular values of
![]() $A\in \mathrm {M}_n$
.
$A\in \mathrm {M}_n$
.
A norm
![]() $\| \cdot \|$
on the
$\| \cdot \|$
on the
![]() $\mathbb {R}$
-vector space
$\mathbb {R}$
-vector space
![]() $\mathrm {H}_n$
of
$\mathrm {H}_n$
of
![]() $n\times n$
complex Hermitian matrices is weakly unitarily invariant if
$n\times n$
complex Hermitian matrices is weakly unitarily invariant if
![]() $\| U^*AU \|=\| A \|$
for all
$\| U^*AU \|=\| A \|$
for all
![]() $A\in \mathrm {H}_n$
and unitary
$A\in \mathrm {H}_n$
and unitary
![]() $U \in \mathrm {M}_n$
. For example, the numerical radius
$U \in \mathrm {M}_n$
. For example, the numerical radius
 $$ \begin{align*} r(A) = \sup_{\mathbf{x} \in {\mathbb{C}}^{n} \backslash \{\mathbf{0}\}} \frac{ \langle A \mathbf{x}, \mathbf{x} \rangle}{\langle \mathbf{x} , \mathbf{x} \rangle}\end{align*} $$
$$ \begin{align*} r(A) = \sup_{\mathbf{x} \in {\mathbb{C}}^{n} \backslash \{\mathbf{0}\}} \frac{ \langle A \mathbf{x}, \mathbf{x} \rangle}{\langle \mathbf{x} , \mathbf{x} \rangle}\end{align*} $$
is a weakly unitarily invariant norm on
![]() $\mathrm {H}_n$
[Reference Li12]. Lewis proved that any weakly unitarily invariant norm on
$\mathrm {H}_n$
[Reference Li12]. Lewis proved that any weakly unitarily invariant norm on
![]() $\mathrm {H}_n$
is a symmetric vector norm applied to the eigenvalues [Reference Lewis11, Section 8].
$\mathrm {H}_n$
is a symmetric vector norm applied to the eigenvalues [Reference Lewis11, Section 8].
Our first result is a short proof of Lewis’ theorem that avoids his theory of group invariance in convex matrix analysis [Reference Lewis11], the wonderful but complicated framework that underpins [Reference Aguilar, Chávez, Garcia and Volčič1, Reference Chávez, Garcia and Hurley7]. Our new approach uses more standard techniques, such as Birkhoff’s theorem on doubly stochastic matrices [Reference Birkhoff6].
Theorem 1.1 A norm
![]() $\| \cdot \|$
on
$\| \cdot \|$
on
![]() $\mathrm {H}_n$
is weakly unitarily invariant if and only if there is a symmetric norm
$\mathrm {H}_n$
is weakly unitarily invariant if and only if there is a symmetric norm
![]() $f:\mathbb {R}^n\to \mathbb {R}$
such that
$f:\mathbb {R}^n\to \mathbb {R}$
such that
![]() $\| A \|=f( \lambda _1, \lambda _2, \ldots , \lambda _n)$
for all
$\| A \|=f( \lambda _1, \lambda _2, \ldots , \lambda _n)$
for all
![]() $A\in \mathrm {H}_n$
. Here,
$A\in \mathrm {H}_n$
. Here,
![]() $\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _n$
are the eigenvalues of A.
$\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _n$
are the eigenvalues of A.
The random-vector norms of the next theorem are weakly unitarily invariant norms on
![]() $\mathrm {H}_n$
that extend to weakly unitarily invariant norms on
$\mathrm {H}_n$
that extend to weakly unitarily invariant norms on
![]() $\mathrm {M}_n$
(see Theorem 1.3). They appeared in [Reference Chávez, Garcia and Hurley7], and they generalize the complete homogeneous symmetric polynomial norms of [Reference Aguilar, Chávez, Garcia and Volčič1, Theorem 1]. The original proof of [Reference Chávez, Garcia and Hurley7, Theorem 1.1(a)] requires
$\mathrm {M}_n$
(see Theorem 1.3). They appeared in [Reference Chávez, Garcia and Hurley7], and they generalize the complete homogeneous symmetric polynomial norms of [Reference Aguilar, Chávez, Garcia and Volčič1, Theorem 1]. The original proof of [Reference Chávez, Garcia and Hurley7, Theorem 1.1(a)] requires
![]() $d \geq 2$
and relies heavily on Lewis’ framework for group invariance in convex matrix analysis [Reference Lewis11]. However, Theorem 1.2 now follows directly from Theorem 1.1. Moreover, Theorem 1.2 generalizes [Reference Chávez, Garcia and Hurley7, Theorem 1.1(a)] to the case
$d \geq 2$
and relies heavily on Lewis’ framework for group invariance in convex matrix analysis [Reference Lewis11]. However, Theorem 1.2 now follows directly from Theorem 1.1. Moreover, Theorem 1.2 generalizes [Reference Chávez, Garcia and Hurley7, Theorem 1.1(a)] to the case
![]() $d\geq 1$
.
$d\geq 1$
.
Theorem 1.2 Let
![]() $d\geq 1$
be real and
$d\geq 1$
be real and
![]() $\mathbf {X}$
be an independent and identically distributed (iid) random vector in
$\mathbf {X}$
be an independent and identically distributed (iid) random vector in
![]() $\mathbb {R}^n$
, that is, the entries of
$\mathbb {R}^n$
, that is, the entries of
![]() $\mathbf {X}=(X_1,X_2, \ldots , X_n)$
are nondegenerate iid random variables. Then
$\mathbf {X}=(X_1,X_2, \ldots , X_n)$
are nondegenerate iid random variables. Then
 $$ \begin{align} ||A||_{{\mathbf{X}},d} = \left(\frac{{\mathbb{E}} |\langle{\mathbf{X}}, \boldsymbol{\lambda}\rangle|^d}{\Gamma(d+1)}\right)^{1/d} \end{align} $$
$$ \begin{align} ||A||_{{\mathbf{X}},d} = \left(\frac{{\mathbb{E}} |\langle{\mathbf{X}}, \boldsymbol{\lambda}\rangle|^d}{\Gamma(d+1)}\right)^{1/d} \end{align} $$
is a weakly unitarily invariant norm on
![]() $\mathrm {H}_n$
. Here,
$\mathrm {H}_n$
. Here,
![]() $\Gamma (\cdot )$
denotes the gamma function and
$\Gamma (\cdot )$
denotes the gamma function and
![]() $\boldsymbol {\lambda }=(\lambda _1,\lambda _2, \ldots , \lambda _n)$
denotes the vector of eigenvalues
$\boldsymbol {\lambda }=(\lambda _1,\lambda _2, \ldots , \lambda _n)$
denotes the vector of eigenvalues
![]() $\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _n$
of A. Moreover, if the entries of
$\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _n$
of A. Moreover, if the entries of
![]() $\mathbf {X}$
each have at least m moments, then for all
$\mathbf {X}$
each have at least m moments, then for all
![]() $A\in \mathrm {H}_n$
the function
$A\in \mathrm {H}_n$
the function
![]() $f:[1,m] \to \mathbb {R}$
defined by
$f:[1,m] \to \mathbb {R}$
defined by
![]() $f(d) =\| A \|_{\mathbf {X},d}$
is continuous.
$f(d) =\| A \|_{\mathbf {X},d}$
is continuous.
The simplified proof of Theorem 1.1 and the extension of Theorem 1.2 from
![]() $d\geq 2$
to
$d\geq 2$
to
![]() $d \geq 1$
permit the main results of [Reference Chávez, Garcia and Hurley7], restated below as Theorem 1.3, to rest on simpler foundations while enjoying a wider range of applicability. The many perspectives offered in Theorem 1.3 explain the normalization in (1.1).
$d \geq 1$
permit the main results of [Reference Chávez, Garcia and Hurley7], restated below as Theorem 1.3, to rest on simpler foundations while enjoying a wider range of applicability. The many perspectives offered in Theorem 1.3 explain the normalization in (1.1).
Theorem 1.3 Let
![]() $\mathbf {X}=(X_1, X_2, \ldots , X_n)$
, in which
$\mathbf {X}=(X_1, X_2, \ldots , X_n)$
, in which
![]() $X_1, X_2, \ldots , X_n \in L^d(\Omega ,\mathcal {F},\mathbb {P})$
are nondegenerate iid random variables. Let
$X_1, X_2, \ldots , X_n \in L^d(\Omega ,\mathcal {F},\mathbb {P})$
are nondegenerate iid random variables. Let
![]() $\boldsymbol {\lambda }=(\lambda _1,\lambda _2, \ldots , \lambda _n)$
denote the vector of eigenvalues
$\boldsymbol {\lambda }=(\lambda _1,\lambda _2, \ldots , \lambda _n)$
denote the vector of eigenvalues
![]() $\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _n$
of
$\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _n$
of
![]() $A \in \mathrm {H}_n$
.
$A \in \mathrm {H}_n$
.
-
(1) For real
 $d\geq 1$
,
$d\geq 1$
,
 $\| A \|_{\mathbf {X},d}= \bigg (\dfrac { \mathbb {E} |\langle \mathbf {X}, \boldsymbol {\lambda }\rangle |^d}{\Gamma (d+1)} \bigg )^{1/d}$
is a norm on
$\| A \|_{\mathbf {X},d}= \bigg (\dfrac { \mathbb {E} |\langle \mathbf {X}, \boldsymbol {\lambda }\rangle |^d}{\Gamma (d+1)} \bigg )^{1/d}$
is a norm on
 $\mathrm {H}_n$
(now by Theorem 1.2).
$\mathrm {H}_n$
(now by Theorem 1.2). -
(2) If the
 $X_i$
admit a moment generating function
$X_i$
admit a moment generating function
 $M(t) = \mathbb {E} [e^{tX}] = \sum _{k=0}^{\infty } \mathbb {E} [X^k] \frac {t^k}{k!}$
and
$M(t) = \mathbb {E} [e^{tX}] = \sum _{k=0}^{\infty } \mathbb {E} [X^k] \frac {t^k}{k!}$
and
 $d \geq 2$
is an even integer, then
$d \geq 2$
is an even integer, then
 $\| A \|_{\mathbf {X},d}^d$
is the coefficient of
$\| A \|_{\mathbf {X},d}^d$
is the coefficient of
 $t^d$
in
$t^d$
in
 $M_{\Lambda }(t)$
for all
$M_{\Lambda }(t)$
for all
 $A \in \mathrm {H}_n$
, in which
$A \in \mathrm {H}_n$
, in which
 $M_{\Lambda }(t) = \prod _{i=1}^n M(\lambda _i t)$
is the moment generating function for the random variable
$M_{\Lambda }(t) = \prod _{i=1}^n M(\lambda _i t)$
is the moment generating function for the random variable
 $\Lambda =\langle \mathbf {X}, \boldsymbol {\lambda }(A) \rangle =\lambda _1X_1+\lambda _2X_2+\cdots +\lambda _n X_n$
. In particular,
$\Lambda =\langle \mathbf {X}, \boldsymbol {\lambda }(A) \rangle =\lambda _1X_1+\lambda _2X_2+\cdots +\lambda _n X_n$
. In particular,
 $\| A \|_{\mathbf {X},d}$
is a positive definite, homogeneous, symmetric polynomial in the eigenvalues of A.
$\| A \|_{\mathbf {X},d}$
is a positive definite, homogeneous, symmetric polynomial in the eigenvalues of A. -
(3) Let
 $d\geq 2$
be an even integer. If the first d moments of
$d\geq 2$
be an even integer. If the first d moments of
 $X_i$
exist, then in which:
$X_i$
exist, then in which: $$ \begin{align*} \| A \|_{\mathbf{X},d}^d = \frac{1}{d!} B_{d}(\kappa_1\operatorname{tr} A, \kappa_2\operatorname{tr} A^2, \ldots, \kappa_d\operatorname{tr} A^d) =\sum_{\boldsymbol{\pi}\vdash d}\frac{\kappa_{\boldsymbol{\pi}}p_{\boldsymbol{\pi}} (\boldsymbol{\lambda})}{y_{\boldsymbol{\pi}}} \quad \text{for }A \in \mathrm{H}_n, \end{align*} $$
$$ \begin{align*} \| A \|_{\mathbf{X},d}^d = \frac{1}{d!} B_{d}(\kappa_1\operatorname{tr} A, \kappa_2\operatorname{tr} A^2, \ldots, \kappa_d\operatorname{tr} A^d) =\sum_{\boldsymbol{\pi}\vdash d}\frac{\kappa_{\boldsymbol{\pi}}p_{\boldsymbol{\pi}} (\boldsymbol{\lambda})}{y_{\boldsymbol{\pi}}} \quad \text{for }A \in \mathrm{H}_n, \end{align*} $$
-
(a)
 $\boldsymbol {\pi }=(\pi _1, \pi _2, \ldots , \pi _r) \in \mathbb {N}^r$
is a partition of d; that is,
$\boldsymbol {\pi }=(\pi _1, \pi _2, \ldots , \pi _r) \in \mathbb {N}^r$
is a partition of d; that is,
 $\pi _1 \geq \pi _2 \geq \cdots \geq \pi _r$
and
$\pi _1 \geq \pi _2 \geq \cdots \geq \pi _r$
and
 $\pi _1+ \pi _2 + \cdots + \pi _r = d$
[Reference Stanley13, Section 1.7]; we denote this
$\pi _1+ \pi _2 + \cdots + \pi _r = d$
[Reference Stanley13, Section 1.7]; we denote this
 $\boldsymbol {\pi } \vdash d$
;
$\boldsymbol {\pi } \vdash d$
; -
(b)
 $p_{\boldsymbol {\pi }}(x_1, x_2, \ldots , x_n)=p_{\pi _1}p_{\pi _2}\cdots p_{\pi _r}$
, in which
$p_{\boldsymbol {\pi }}(x_1, x_2, \ldots , x_n)=p_{\pi _1}p_{\pi _2}\cdots p_{\pi _r}$
, in which
 $p_k(x_1,x_2, \ldots , x_n)=x_1^k+x_2^k+\cdots +x_n^k$
is a power-sum symmetric polynomial;
$p_k(x_1,x_2, \ldots , x_n)=x_1^k+x_2^k+\cdots +x_n^k$
is a power-sum symmetric polynomial; -
(c)
 $B_d$
is a complete Bell polynomial, defined by
$B_d$
is a complete Bell polynomial, defined by
 $\sum _{\ell =0}^{\infty } B_{\ell }(x_1, x_2, \ldots , x_{\ell }) \frac {t^{\ell }}{\ell !} =\exp ( \sum _{j=1}^{\infty } x_j \frac {t^j}{j!})$
[Reference Bell2, Section II];
$\sum _{\ell =0}^{\infty } B_{\ell }(x_1, x_2, \ldots , x_{\ell }) \frac {t^{\ell }}{\ell !} =\exp ( \sum _{j=1}^{\infty } x_j \frac {t^j}{j!})$
[Reference Bell2, Section II]; -
(d) The cumulants
 $\kappa _1, \kappa _2, \ldots , \kappa _d$
are defined by the recursion
$\kappa _1, \kappa _2, \ldots , \kappa _d$
are defined by the recursion
 $\mu _r=\sum _{\ell =0}^{r-1}{r-1\choose \ell } \mu _{\ell }\kappa _{r-\ell }$
for
$\mu _r=\sum _{\ell =0}^{r-1}{r-1\choose \ell } \mu _{\ell }\kappa _{r-\ell }$
for
 $1 \leq r \leq d$
, in which
$1 \leq r \leq d$
, in which
 $\mu _r = \mathbb {E}[X_1^r]$
is the rth moment of
$\mu _r = \mathbb {E}[X_1^r]$
is the rth moment of
 $X_1$
[Reference Billingsley5, Section 9]; and
$X_1$
[Reference Billingsley5, Section 9]; and -
(e)
 $\kappa _{\boldsymbol {\pi }} = \kappa _{\pi _1} \kappa _{\pi _2} \cdots \kappa _{\pi _{r}}$
and
$\kappa _{\boldsymbol {\pi }} = \kappa _{\pi _1} \kappa _{\pi _2} \cdots \kappa _{\pi _{r}}$
and
 $y_{\boldsymbol {\pi }}=\prod _{i\geq 1}(i!)^{m_i}m_i!$
, in which
$y_{\boldsymbol {\pi }}=\prod _{i\geq 1}(i!)^{m_i}m_i!$
, in which
 $m_i=m_i(\boldsymbol {\pi })$
is the multiplicity of i in
$m_i=m_i(\boldsymbol {\pi })$
is the multiplicity of i in
 $\boldsymbol {\pi }$
.
$\boldsymbol {\pi }$
.
-
-
(4) For real
 $d\geq 1$
, the function
$d\geq 1$
, the function
 $\boldsymbol {\lambda }(A) \mapsto \| A \|_{\mathbf {X},d}$
is Schur convex; that is, it respects majorization
$\boldsymbol {\lambda }(A) \mapsto \| A \|_{\mathbf {X},d}$
is Schur convex; that is, it respects majorization
 $\prec $
(see (3.1)).
$\prec $
(see (3.1)). -
(5) Let
 $d\geq 2$
be an even integer. Define
$d\geq 2$
be an even integer. Define
 $\mathrm {T}_{\boldsymbol {\pi }} : \mathrm {M}_{n}\to \mathbb {R}$
by setting
$\mathrm {T}_{\boldsymbol {\pi }} : \mathrm {M}_{n}\to \mathbb {R}$
by setting
 $\mathrm {T}_{\boldsymbol {\pi }}(Z)$
to be
$\mathrm {T}_{\boldsymbol {\pi }}(Z)$
to be
 $1/{d\choose d/2}$
times the sum over the
$1/{d\choose d/2}$
times the sum over the
 $\binom {d}{d/2}$
possible locations to place
$\binom {d}{d/2}$
possible locations to place
 $d/2$
adjoints
$d/2$
adjoints
 ${}^*$
among the d copies of Z in
${}^*$
among the d copies of Z in
 $(\operatorname {tr} \underbrace {ZZ\cdots Z}_{\pi _1}) (\operatorname {tr} \underbrace {ZZ\cdots Z}_{\pi _2}) \cdots (\operatorname {tr} \underbrace {ZZ\cdots Z}_{\pi _r})$
. Then (1.2)is a norm on
$(\operatorname {tr} \underbrace {ZZ\cdots Z}_{\pi _1}) (\operatorname {tr} \underbrace {ZZ\cdots Z}_{\pi _2}) \cdots (\operatorname {tr} \underbrace {ZZ\cdots Z}_{\pi _r})$
. Then (1.2)is a norm on $$ \begin{align} \| Z \|_{\mathbf{X},d}= \bigg( \sum_{\boldsymbol{\pi} \,\vdash\, d} \frac{ \kappa_{\boldsymbol{\pi}}\mathrm{T}_{\boldsymbol{\pi}}(Z)}{y_{\boldsymbol{\pi}}}\bigg)^{1/d}\end{align} $$
$$ \begin{align} \| Z \|_{\mathbf{X},d}= \bigg( \sum_{\boldsymbol{\pi} \,\vdash\, d} \frac{ \kappa_{\boldsymbol{\pi}}\mathrm{T}_{\boldsymbol{\pi}}(Z)}{y_{\boldsymbol{\pi}}}\bigg)^{1/d}\end{align} $$
 $\mathrm {M}_n$
that restricts to the norm on
$\mathrm {M}_n$
that restricts to the norm on
 $\mathrm {H}_n$
above. In particular,
$\mathrm {H}_n$
above. In particular,
 $\| Z \|_{\mathbf {X},d}^d$
is a positive definite trace polynomial in Z and
$\| Z \|_{\mathbf {X},d}^d$
is a positive definite trace polynomial in Z and
 $Z^*$
.
$Z^*$
.
The paper is structured as follows. Section 2 provides several examples afforded by the theorems above. The proofs of Theorems 1.1 and 1.2 appear in Sections 3 and 4, respectively. Section 5 concludes with some brief remarks.
2 Examples
The norm
![]() $\| \cdot \|_{\mathbf {X},d}$
defined in (1.1) is determined by its unit ball. This provides one way to visualize the properties of random vector norms. We consider a few examples hereand refer the reader to [Reference Chávez, Garcia and Hurley7, Section 2] for further examples and details.
$\| \cdot \|_{\mathbf {X},d}$
defined in (1.1) is determined by its unit ball. This provides one way to visualize the properties of random vector norms. We consider a few examples hereand refer the reader to [Reference Chávez, Garcia and Hurley7, Section 2] for further examples and details.
2.1 Normal random variables
Suppose
![]() $d\geq 2$
is an even integer and
$d\geq 2$
is an even integer and
![]() $\mathbf {X}$
is a random vector whose entries are independent normal random variables with mean
$\mathbf {X}$
is a random vector whose entries are independent normal random variables with mean
![]() $\mu $
and variance
$\mu $
and variance
![]() $\sigma ^2$
. The example in [Reference Chávez, Garcia and Hurley7, equation (2.12)] illustrates
$\sigma ^2$
. The example in [Reference Chávez, Garcia and Hurley7, equation (2.12)] illustrates
 $$ \begin{align*} \| A \|_{\mathbf{X},d}^d=\sum_{k=0}^{\frac{d}{2}} \frac{\mu^{2k} (\operatorname{tr} A)^{2k}}{(2k)!} \cdot \frac{\sigma^{d-2k} \| A\|_{\operatorname{F}}^{d-2k}}{2^{\frac{d}{2}-k} (\frac{d}{2}-k)!} \quad \text{for }A \in \mathrm{H}_n, \end{align*} $$
$$ \begin{align*} \| A \|_{\mathbf{X},d}^d=\sum_{k=0}^{\frac{d}{2}} \frac{\mu^{2k} (\operatorname{tr} A)^{2k}}{(2k)!} \cdot \frac{\sigma^{d-2k} \| A\|_{\operatorname{F}}^{d-2k}}{2^{\frac{d}{2}-k} (\frac{d}{2}-k)!} \quad \text{for }A \in \mathrm{H}_n, \end{align*} $$
in which
![]() $\| \cdot \|_{\operatorname {F}}$
is the Frobenius norm. For
$\| \cdot \|_{\operatorname {F}}$
is the Frobenius norm. For
![]() $d=2$
, the extension to
$d=2$
, the extension to
![]() $\mathrm {M}_n$
guaranteed by Theorem 1.3 is
$\mathrm {M}_n$
guaranteed by Theorem 1.3 is
![]() $\| Z \|_{\mathbf {X},2}^2= \tfrac {1}{2} \sigma ^2 \operatorname {tr}(Z^*\!Z) + \tfrac {1}{2} \mu ^2 (\operatorname {tr} Z^*)(\operatorname {tr} Z)$
[Reference Chávez, Garcia and Hurley7, p. 816].
$\| Z \|_{\mathbf {X},2}^2= \tfrac {1}{2} \sigma ^2 \operatorname {tr}(Z^*\!Z) + \tfrac {1}{2} \mu ^2 (\operatorname {tr} Z^*)(\operatorname {tr} Z)$
[Reference Chávez, Garcia and Hurley7, p. 816].
Now, let
![]() $n=2$
. If
$n=2$
. If
![]() $\mu =0$
, the restrictions of
$\mu =0$
, the restrictions of
![]() $\| \cdot \|_{\mathbf {X},d}$
to
$\| \cdot \|_{\mathbf {X},d}$
to
![]() $\mathbb {R}^2$
(whose elements are identified with diagonal matrices) reproduce multiples of the Euclidean norm. If
$\mathbb {R}^2$
(whose elements are identified with diagonal matrices) reproduce multiples of the Euclidean norm. If
![]() $\mu \neq 0$
, then the unit circles for
$\mu \neq 0$
, then the unit circles for
![]() $\| \cdot \|_{\mathbf {X},d}$
are approximately elliptical (see Figure 1).
$\| \cdot \|_{\mathbf {X},d}$
are approximately elliptical (see Figure 1).

Figure 1
(Left) Unit circles for
![]() $\|\cdot \|_{\mathbf {X},d}$
with
$\|\cdot \|_{\mathbf {X},d}$
with
![]() $d=1, 2, 4, 20$
, in which
$d=1, 2, 4, 20$
, in which
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are standard normal random variables. (Right) Unit circles for
$X_2$
are standard normal random variables. (Right) Unit circles for
![]() $\|\cdot \|_{\mathbf {X},10}$
, in which
$\|\cdot \|_{\mathbf {X},10}$
, in which
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are normal random variables with means
$X_2$
are normal random variables with means
![]() $\mu =-2, -1, 0, 1, 6$
and variance
$\mu =-2, -1, 0, 1, 6$
and variance
![]() $\sigma ^2=1$
.
$\sigma ^2=1$
.
2.2 Standard exponential random variables
If
![]() $d\geq 2$
is an even integer and
$d\geq 2$
is an even integer and
![]() $\mathbf {X}$
is a random vector whose entries are independent standard exponential random variables, then
$\mathbf {X}$
is a random vector whose entries are independent standard exponential random variables, then
![]() $\| A \|_{\mathbf {X},d}^d$
equals the complete homogeneous symmetric polynomial
$\| A \|_{\mathbf {X},d}^d$
equals the complete homogeneous symmetric polynomial
![]() $h_d(\lambda _1, \lambda _2, \ldots , \lambda _n)=\sum _{1\leq k_1\leq \cdots \leq k_d\leq n} \lambda _{k_1}\lambda _{k_2}\cdots \lambda _{k_d}$
in the eigenvalues
$h_d(\lambda _1, \lambda _2, \ldots , \lambda _n)=\sum _{1\leq k_1\leq \cdots \leq k_d\leq n} \lambda _{k_1}\lambda _{k_2}\cdots \lambda _{k_d}$
in the eigenvalues
![]() $\lambda _1, \lambda _2, \ldots , \lambda _n$
[Reference Aguilar, Chávez, Garcia and Volčič1]. For
$\lambda _1, \lambda _2, \ldots , \lambda _n$
[Reference Aguilar, Chávez, Garcia and Volčič1]. For
![]() $d=4$
, the extension to
$d=4$
, the extension to
![]() $\mathrm {M}_n$
guaranteed by Theorem 1.3 is [Reference Aguilar, Chávez, Garcia and Volčič1, equation (9)]
$\mathrm {M}_n$
guaranteed by Theorem 1.3 is [Reference Aguilar, Chávez, Garcia and Volčič1, equation (9)]
 $$ \begin{align*} \| Z \|_4^4 &= \frac{1}{24} \big( (\operatorname{tr} Z)^2 \operatorname{tr}(Z^*)^2 + \operatorname{tr}(Z^*)^2 \operatorname{tr}(Z^2) + 4 \operatorname{tr}(Z)\operatorname{tr}(Z^*) \operatorname{tr}(Z^*Z) \nonumber \\ & \qquad + 2 \operatorname{tr}(Z^*Z)^2 + (\operatorname{tr} Z)^2 \operatorname{tr}(Z^{*2}) + \operatorname{tr}(Z^2) \operatorname{tr}(Z^{*2}) + 4\operatorname{tr}(Z^*) \operatorname{tr}(Z^*Z^2) \nonumber \\ & \qquad + 4 \operatorname{tr}(Z) \operatorname{tr}(Z^{*2}Z) + 2 \operatorname{tr}(Z^*ZZ^*Z) + 4 \operatorname{tr}(Z^{*2}Z^2) \big). \end{align*} $$
$$ \begin{align*} \| Z \|_4^4 &= \frac{1}{24} \big( (\operatorname{tr} Z)^2 \operatorname{tr}(Z^*)^2 + \operatorname{tr}(Z^*)^2 \operatorname{tr}(Z^2) + 4 \operatorname{tr}(Z)\operatorname{tr}(Z^*) \operatorname{tr}(Z^*Z) \nonumber \\ & \qquad + 2 \operatorname{tr}(Z^*Z)^2 + (\operatorname{tr} Z)^2 \operatorname{tr}(Z^{*2}) + \operatorname{tr}(Z^2) \operatorname{tr}(Z^{*2}) + 4\operatorname{tr}(Z^*) \operatorname{tr}(Z^*Z^2) \nonumber \\ & \qquad + 4 \operatorname{tr}(Z) \operatorname{tr}(Z^{*2}Z) + 2 \operatorname{tr}(Z^*ZZ^*Z) + 4 \operatorname{tr}(Z^{*2}Z^2) \big). \end{align*} $$
The unit balls for these norms are illustrated in Figure 2 (left).

Figure 2
(Left) Unit circles for
![]() $\|\cdot \|_{\mathbf {X},d}$
with
$\|\cdot \|_{\mathbf {X},d}$
with
![]() $d=1, 2, 3, 4, 20$
, in which
$d=1, 2, 3, 4, 20$
, in which
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are standard exponentials. (Right) Unit circles for
$X_2$
are standard exponentials. (Right) Unit circles for
![]() $\| \cdot \|_{\mathbf {X},d}$
with
$\| \cdot \|_{\mathbf {X},d}$
with
![]() $d=2, 4, 20$
, in which
$d=2, 4, 20$
, in which
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are Bernoulli with
$X_2$
are Bernoulli with
![]() $q=0.5$
.
$q=0.5$
.
2.3 Bernoulli random variables
A Bernoulli random variable is a discrete random variable X defined according to
![]() $\mathbb {P}(X=k)=q^k(1-q)^{1-k}$
for
$\mathbb {P}(X=k)=q^k(1-q)^{1-k}$
for
![]() $k=0,1$
and
$k=0,1$
and
![]() $0<q<1$
. Suppose d is an even integer and
$0<q<1$
. Suppose d is an even integer and
![]() $\mathbf {X}$
is a random vector whose entries are independental Bernoulli random variables with parameter q.
$\mathbf {X}$
is a random vector whose entries are independental Bernoulli random variables with parameter q.
Remark 2.1 An expression for
![]() $\| A \|^d_{\mathbf {X},d}$
appears in [Reference Chávez, Garcia and Hurley7, Section 2.7]. However, there is a missing multinomial coefficient. The correct expression for
$\| A \|^d_{\mathbf {X},d}$
appears in [Reference Chávez, Garcia and Hurley7, Section 2.7]. However, there is a missing multinomial coefficient. The correct expression for
![]() $\| A \|^d_{\mathbf {X},d}$
is given by
$\| A \|^d_{\mathbf {X},d}$
is given by
 $$ \begin{align*} \| A \|^d_{\mathbf{X},d}=\frac{1}{d!}\sum_{i_1+i_2+\cdots+i_n=d} \binom{d}{i_1,i_2,\ldots,i_n}q^{|I|} \lambda_1^{i_1}\lambda_2^{i_2}\cdots \lambda_n^{i_n}, \end{align*}$$
$$ \begin{align*} \| A \|^d_{\mathbf{X},d}=\frac{1}{d!}\sum_{i_1+i_2+\cdots+i_n=d} \binom{d}{i_1,i_2,\ldots,i_n}q^{|I|} \lambda_1^{i_1}\lambda_2^{i_2}\cdots \lambda_n^{i_n}, \end{align*}$$
in which
![]() $|I|$
is the number of nonzero
$|I|$
is the number of nonzero
![]() $i_k$
; that is,
$i_k$
; that is,
![]() $I = \{ k : i_k \neq 0\}$
. We thank the anonymous referee for pointing out the typo in [Reference Chávez, Garcia and Hurley7, Section 2.7]. Figures 2 (right) and 3 illustrate the unit balls for these norms in a variety of cases.
$I = \{ k : i_k \neq 0\}$
. We thank the anonymous referee for pointing out the typo in [Reference Chávez, Garcia and Hurley7, Section 2.7]. Figures 2 (right) and 3 illustrate the unit balls for these norms in a variety of cases.

Figure 3 Unit circles for
![]() $\|\cdot \|_{\mathbf {X},d}$
, in which
$\|\cdot \|_{\mathbf {X},d}$
, in which
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are Bernoulli with varying parameter q and with
$X_2$
are Bernoulli with varying parameter q and with
![]() $d=2$
(left) and
$d=2$
(left) and
![]() $d=10$
(right).
$d=10$
(right).
2.4 Pareto random variables
Suppose
![]() $\alpha , x_m>0$
. A random variable X distributed according to the probability density function
$\alpha , x_m>0$
. A random variable X distributed according to the probability density function
 $$ \begin{align*} f_X(t)= \begin{cases} \dfrac{\alpha x_m^{\alpha}}{t^{\alpha+1}}, & \text{if}\ t\geq x_m,\\ 0, & \text{if}\ t<x_m, \end{cases} \end{align*} $$
$$ \begin{align*} f_X(t)= \begin{cases} \dfrac{\alpha x_m^{\alpha}}{t^{\alpha+1}}, & \text{if}\ t\geq x_m,\\ 0, & \text{if}\ t<x_m, \end{cases} \end{align*} $$
is a Pareto random variable with parameters
![]() $\alpha $
and
$\alpha $
and
![]() $x_m$
. Suppose
$x_m$
. Suppose
![]() $\mathbf {X}$
is a random vector whose entries are Pareto random variables. Then
$\mathbf {X}$
is a random vector whose entries are Pareto random variables. Then
![]() $\| A \|_{\mathbf {X},d}$
exists whenever
$\| A \|_{\mathbf {X},d}$
exists whenever
![]() $\alpha>d$
[Reference Chávez, Garcia and Hurley7, Section 2.10].
$\alpha>d$
[Reference Chávez, Garcia and Hurley7, Section 2.10].
Suppose
![]() $d=2$
and
$d=2$
and
![]() $\mathbf {X}$
is a random vector whose entries are independent Pareto random variables with
$\mathbf {X}$
is a random vector whose entries are independent Pareto random variables with
![]() $\alpha>2$
and
$\alpha>2$
and
![]() $x_m=1$
. If
$x_m=1$
. If
![]() $n=2$
, then
$n=2$
, then
 $$ \begin{align*} \| A \|_{\mathbf{X},2}^2=\frac{\alpha}{2}\Bigg( \frac{\lambda_1^2}{\alpha-2}+\frac{2\alpha \lambda_1\lambda_2}{(\alpha-1)^2}+\frac{\lambda_2^2}{\alpha-2} \Bigg).\end{align*} $$
$$ \begin{align*} \| A \|_{\mathbf{X},2}^2=\frac{\alpha}{2}\Bigg( \frac{\lambda_1^2}{\alpha-2}+\frac{2\alpha \lambda_1\lambda_2}{(\alpha-1)^2}+\frac{\lambda_2^2}{\alpha-2} \Bigg).\end{align*} $$
Figure 4 (left) illustrates the unit circles for
![]() $\| \cdot \|_{\mathbf {X},2}$
with varying
$\| \cdot \|_{\mathbf {X},2}$
with varying
![]() $\alpha $
. As
$\alpha $
. As
![]() $\alpha \to \infty $
, the unit circles approach the parallel lines at
$\alpha \to \infty $
, the unit circles approach the parallel lines at
![]() $\lambda _2=\pm \sqrt {2}-\lambda _1$
; that is,
$\lambda _2=\pm \sqrt {2}-\lambda _1$
; that is,
![]() $|\operatorname {tr} A|^2 = 2$
. Figure 4 (right) depicts the unit circles for
$|\operatorname {tr} A|^2 = 2$
. Figure 4 (right) depicts the unit circles for
![]() $\| \cdot \|_{\mathbf {X},d}$
with fixed
$\| \cdot \|_{\mathbf {X},d}$
with fixed
![]() $\alpha $
and varying d.
$\alpha $
and varying d.

Figure 4
(Left) Unit circles for
![]() $\| \cdot \|_{\mathbf {X},2}$
, in which
$\| \cdot \|_{\mathbf {X},2}$
, in which
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are independent Pareto random variables with
$X_2$
are independent Pareto random variables with
![]() $\alpha =2.1, 3, 4, 10$
and
$\alpha =2.1, 3, 4, 10$
and
![]() $x_m=1$
. (Right) Unit circles for
$x_m=1$
. (Right) Unit circles for
![]() $\| \cdot \|_{\mathbf {X},d}$
, in which
$\| \cdot \|_{\mathbf {X},d}$
, in which
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are independent Pareto random variables with
$X_2$
are independent Pareto random variables with
![]() $\alpha =5$
and
$\alpha =5$
and
![]() $p=1, 2, 4$
.
$p=1, 2, 4$
.
3 Proof of Theorem 1.1
The proof of Theorem 1.1 follows from Propositions 3.1 and 3.5.
Proposition 3.1 If
![]() $\| \cdot \|$
is a weakly unitarily invariant norm on
$\| \cdot \|$
is a weakly unitarily invariant norm on
![]() $\mathrm {H}_n$
, then there is a symmetric norm f on
$\mathrm {H}_n$
, then there is a symmetric norm f on
![]() $\mathbb {R}^n$
such that
$\mathbb {R}^n$
such that
![]() $\| A \|=f( \boldsymbol {\lambda }(A))$
for all
$\| A \|=f( \boldsymbol {\lambda }(A))$
for all
![]() $A\in \mathrm {H}_n$
.
$A\in \mathrm {H}_n$
.
Proof Hermitian matrices are unitarily diagonalizable. Since
![]() $\| \cdot \|$
is weakly unitarily invariant,
$\| \cdot \|$
is weakly unitarily invariant,
![]() $\| A \|=\| D \|$
, in which D is a diagonalization of A. Consequently,
$\| A \|=\| D \|$
, in which D is a diagonalization of A. Consequently,
![]() $\| A \|$
must be a function in the eigenvalues of A. Moreover, any permutation of the entries in D is obtained by conjugating D by a permutation matrix, which is unitary. Therefore,
$\| A \|$
must be a function in the eigenvalues of A. Moreover, any permutation of the entries in D is obtained by conjugating D by a permutation matrix, which is unitary. Therefore,
![]() $\| A \|$
is a symmetric function in the eigenvalues of A. In particular,
$\| A \|$
is a symmetric function in the eigenvalues of A. In particular,
![]() $\| A \|=f( \boldsymbol {\lambda }(A) )$
for some symmetric function f. Given
$\| A \|=f( \boldsymbol {\lambda }(A) )$
for some symmetric function f. Given
![]() $\mathbf {a}=( a_1, a_2,\dots , a_n)\in \mathbb {R}^n$
, define the Hermitian matrix
$\mathbf {a}=( a_1, a_2,\dots , a_n)\in \mathbb {R}^n$
, define the Hermitian matrix
 $$ \begin{align*} \operatorname{diag}{\mathbf{a}} = \begin{bmatrix} a_1 & & &\\ & a_2 & &\\ & & \ddots & \\ & & & a_n \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \operatorname{diag}{\mathbf{a}} = \begin{bmatrix} a_1 & & &\\ & a_2 & &\\ & & \ddots & \\ & & & a_n \end{bmatrix}. \end{align*} $$
Then
![]() $\boldsymbol {\lambda }(\operatorname {diag}{\mathbf {a}}) = P\mathbf {a}$
for some permutation matrix P. Symmetry of f implies
$\boldsymbol {\lambda }(\operatorname {diag}{\mathbf {a}}) = P\mathbf {a}$
for some permutation matrix P. Symmetry of f implies
Consequently, f inherits the defining properties of a norm on
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
Let
![]() $\widetilde {\mathbf {x}}=(\widetilde {x}_1,\widetilde {x}_2, \ldots , \widetilde {x}_n)$
denote the nondecreasing rearrangement of
$\widetilde {\mathbf {x}}=(\widetilde {x}_1,\widetilde {x}_2, \ldots , \widetilde {x}_n)$
denote the nondecreasing rearrangement of
![]() $\mathbf {x}= (x_1, x_2, \ldots , x_n)\in \mathbb {R}^n$
. Then
$\mathbf {x}= (x_1, x_2, \ldots , x_n)\in \mathbb {R}^n$
. Then
![]() $\mathbf {y}$
majorizes
$\mathbf {y}$
majorizes
![]() $\mathbf {x}$
, denoted
$\mathbf {x}$
, denoted
![]() $\mathbf {x}\prec \mathbf {y}$
, if
$\mathbf {x}\prec \mathbf {y}$
, if
 $$ \begin{align} \sum_{i=1}^n \widetilde{x}_i=\sum_{i=1}^n \widetilde{y}_i \quad \text{and} \quad\sum_{i=1}^k \widetilde{x}_i\leq \sum_{i=1}^k \widetilde{y}_i \quad \text{for }1 \leq k\leq n-1. \end{align} $$
$$ \begin{align} \sum_{i=1}^n \widetilde{x}_i=\sum_{i=1}^n \widetilde{y}_i \quad \text{and} \quad\sum_{i=1}^k \widetilde{x}_i\leq \sum_{i=1}^k \widetilde{y}_i \quad \text{for }1 \leq k\leq n-1. \end{align} $$
Recall that a matrix with nonnegative entries is doubly stochastic if each row and column sums to
![]() $1$
. The next result is due to Hardy, Littlewood, and Pólya [Reference Hardy, Littlewood and Pólya9].
$1$
. The next result is due to Hardy, Littlewood, and Pólya [Reference Hardy, Littlewood and Pólya9].
Lemma 3.2 If
![]() $\mathbf {x}\prec \mathbf {y}$
, then there exists a doubly stochastic matrix D such that
$\mathbf {x}\prec \mathbf {y}$
, then there exists a doubly stochastic matrix D such that
![]() $\mathbf {y} = D \mathbf {x}$
.
$\mathbf {y} = D \mathbf {x}$
.
The next lemma is Birkhoff’s [Reference Birkhoff6];
![]() $n^2-n+1$
works in place of
$n^2-n+1$
works in place of
![]() $n^2$
[Reference Horn and Johnson10, Theorem 8.7.2].
$n^2$
[Reference Horn and Johnson10, Theorem 8.7.2].
Lemma 3.3 If
![]() $D \in \mathrm {M}_n$
is doubly stochastic, then there exist permutation matrices
$D \in \mathrm {M}_n$
is doubly stochastic, then there exist permutation matrices
![]() $P_1,P_2,\ldots ,P_{n^2} \in \mathrm {M}_n$
and nonnegative numbers
$P_1,P_2,\ldots ,P_{n^2} \in \mathrm {M}_n$
and nonnegative numbers
![]() $c_1,c_2,\ldots ,c_{n^2}$
satisfying
$c_1,c_2,\ldots ,c_{n^2}$
satisfying
![]() $\sum _{i=1}^{n^2} c_i = 1$
such that
$\sum _{i=1}^{n^2} c_i = 1$
such that
![]() $D = \sum _{i=1}^{n^2} c_i P_i$
.
$D = \sum _{i=1}^{n^2} c_i P_i$
.
For each
![]() $A \in \mathrm {H}_n$
, recall that
$A \in \mathrm {H}_n$
, recall that
![]() $\boldsymbol {\lambda }(A)=(\lambda _1(A),\lambda _2(A), \ldots , \lambda _n(A))$
denotes the vector of eigenvalues
$\boldsymbol {\lambda }(A)=(\lambda _1(A),\lambda _2(A), \ldots , \lambda _n(A))$
denotes the vector of eigenvalues
![]() $\lambda _1(A) \geq \lambda _2(A) \geq \cdots \geq \lambda _n(A)$
. We regard
$\lambda _1(A) \geq \lambda _2(A) \geq \cdots \geq \lambda _n(A)$
. We regard
![]() $\boldsymbol {\lambda }(A)$
as a column vector for purposes of matrix multiplication.
$\boldsymbol {\lambda }(A)$
as a column vector for purposes of matrix multiplication.
Lemma 3.4 If
![]() $A, B\in \mathrm {H}_n$
, then there exist permutation matrices
$A, B\in \mathrm {H}_n$
, then there exist permutation matrices
![]() $P_1,P_2,\ldots ,P_{n^2} \in \mathrm {M}_n$
and
$P_1,P_2,\ldots ,P_{n^2} \in \mathrm {M}_n$
and
![]() $c_1,c_2,\ldots ,c_{n^2}\geq 0$
such that
$c_1,c_2,\ldots ,c_{n^2}\geq 0$
such that
 $$ \begin{align*} \boldsymbol{\lambda}(A+B) = \sum_{i = 1}^{n^2} c_{i} P_i(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B)) \quad \text{and}\quad \sum_{i = 1}^{n^2} c_i = 1. \end{align*}$$
$$ \begin{align*} \boldsymbol{\lambda}(A+B) = \sum_{i = 1}^{n^2} c_{i} P_i(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B)) \quad \text{and}\quad \sum_{i = 1}^{n^2} c_i = 1. \end{align*}$$
Proof The Ky Fan eigenvalue inequality [Reference Fan8] asserts that
 $$ \begin{align} \sum_{i=1}^{k} \lambda_i(A+B) \leq \sum_{i=1}^{k} \big(\lambda_i(A) + \lambda_i(B)\big) \quad \text{for all }1\leq k\leq n. \end{align} $$
$$ \begin{align} \sum_{i=1}^{k} \lambda_i(A+B) \leq \sum_{i=1}^{k} \big(\lambda_i(A) + \lambda_i(B)\big) \quad \text{for all }1\leq k\leq n. \end{align} $$
The sum of the eigenvalues of a matrix is its trace. Consequently,
 $$ \begin{align*} \sum_{i=1}^{n} \lambda_i(A+B) = \operatorname{tr} (A+B) = \operatorname{tr} A + \operatorname{tr} B = \sum_{i=1}^{n} \big(\lambda_i(A) + \lambda_i(B)\big), \end{align*}$$
$$ \begin{align*} \sum_{i=1}^{n} \lambda_i(A+B) = \operatorname{tr} (A+B) = \operatorname{tr} A + \operatorname{tr} B = \sum_{i=1}^{n} \big(\lambda_i(A) + \lambda_i(B)\big), \end{align*}$$
so equality holds in (3.2) for
![]() $k=n$
. Thus,
$k=n$
. Thus,
![]() $\boldsymbol {\lambda }(A+B) \prec \boldsymbol {\lambda }(A) + \boldsymbol {\lambda }(B)$
. Lemma 3.2 provides a doubly stochastic matrix D such that
$\boldsymbol {\lambda }(A+B) \prec \boldsymbol {\lambda }(A) + \boldsymbol {\lambda }(B)$
. Lemma 3.2 provides a doubly stochastic matrix D such that
![]() $\boldsymbol {\lambda }(A+B) = D(\boldsymbol {\lambda }(A) + \boldsymbol {\lambda }(B))$
. Lemma 3.3 provides the desired permutation matrices and nonnegative scalars.
$\boldsymbol {\lambda }(A+B) = D(\boldsymbol {\lambda }(A) + \boldsymbol {\lambda }(B))$
. Lemma 3.3 provides the desired permutation matrices and nonnegative scalars.
The following proposition completes the proof of Theorem 1.1.
Proposition 3.5 If f is a symmetric norm on
![]() $\mathbb {R}^n$
, then
$\mathbb {R}^n$
, then
![]() $\| A \|=f(\boldsymbol {\lambda }(A))$
defines a weakly unitarily invariant norm on
$\| A \|=f(\boldsymbol {\lambda }(A))$
defines a weakly unitarily invariant norm on
![]() $\mathrm {H}_n$
.
$\mathrm {H}_n$
.
Proof The function
![]() $\| A \|=f(\boldsymbol {\lambda }(A))$
is symmetric in the eigenvalues of A, so it is weakly unitarily invariant. It remains to show that
$\| A \|=f(\boldsymbol {\lambda }(A))$
is symmetric in the eigenvalues of A, so it is weakly unitarily invariant. It remains to show that
![]() $\| \cdot \|$
defines a norm on
$\| \cdot \|$
defines a norm on
![]() $\mathrm {H}_n$
.
$\mathrm {H}_n$
.
Positive definiteness. A Hermitian matrix
![]() $A = 0$
if and only if
$A = 0$
if and only if
![]() $\boldsymbol {\lambda }(A) = 0$
. Thus, the positive definiteness of f implies the positive definiteness of
$\boldsymbol {\lambda }(A) = 0$
. Thus, the positive definiteness of f implies the positive definiteness of
![]() $\| \cdot \|$
.
$\| \cdot \|$
.
Homogeneity. If
![]() $c\geq 0$
, then
$c\geq 0$
, then
![]() $\boldsymbol {\lambda }(cA) = c\boldsymbol {\lambda }(A)$
. If
$\boldsymbol {\lambda }(cA) = c\boldsymbol {\lambda }(A)$
. If
![]() $c<0$
, then
$c<0$
, then
 $$ \begin{align*} \boldsymbol{\lambda}(cA) = c \begin{bmatrix} && 1 \\ & \unicode{x22F0} & \\ 1 & & \end{bmatrix} \boldsymbol{\lambda}(A). \end{align*} $$
$$ \begin{align*} \boldsymbol{\lambda}(cA) = c \begin{bmatrix} && 1 \\ & \unicode{x22F0} & \\ 1 & & \end{bmatrix} \boldsymbol{\lambda}(A). \end{align*} $$
Then the homogeneity and symmetry of f imply that
Triangle inequality. Suppose that
![]() $A,B \in \mathrm {H}_n$
. Lemma 3.4 ensures that there exist permutation matrices
$A,B \in \mathrm {H}_n$
. Lemma 3.4 ensures that there exist permutation matrices
![]() $P_1,P_2,\ldots ,P_{n^2} \in \mathrm {M}_n$
and nonnegative numbers
$P_1,P_2,\ldots ,P_{n^2} \in \mathrm {M}_n$
and nonnegative numbers
![]() $c_1,c_2,\ldots ,c_{n^2}$
satisfying
$c_1,c_2,\ldots ,c_{n^2}$
satisfying
![]() $\sum _{i=1}^{n^2} c_i = 1$
such that
$\sum _{i=1}^{n^2} c_i = 1$
such that
![]() $D = \sum _{i=1}^{n^2} c_i P_i$
. Thus,
$D = \sum _{i=1}^{n^2} c_i P_i$
. Thus,
 $$ \begin{align*} \| A + B \| = f\big(\boldsymbol{\lambda}(A+B)\big) = f\Bigg(\sum_{i = 1}^{n^2} c_{i} P_i\big(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B)\big)\Bigg). \end{align*}$$
$$ \begin{align*} \| A + B \| = f\big(\boldsymbol{\lambda}(A+B)\big) = f\Bigg(\sum_{i = 1}^{n^2} c_{i} P_i\big(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B)\big)\Bigg). \end{align*}$$
The triangle inequality and homogeneity of f yield
 $$ \begin{align} \| A+B \|\leq \sum_{i=1}^{n^2} c_{i} f\big( P_i(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B))\big). \end{align} $$
$$ \begin{align} \| A+B \|\leq \sum_{i=1}^{n^2} c_{i} f\big( P_i(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B))\big). \end{align} $$
Since f is permutation invariant and
![]() $\sum _{i = 1}^{n^2} c_i = 1$
,
$\sum _{i = 1}^{n^2} c_i = 1$
,
 $$ \begin{align*} \sum_{i=1}^{n^2} c_{i} f\big( P_i(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B))\big) = \sum_{i=1}^{n^2} c_{i} f\big(\boldsymbol{\lambda}(A) +\boldsymbol{\lambda}(B)\big)= f\big(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B)\big). \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{n^2} c_{i} f\big( P_i(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B))\big) = \sum_{i=1}^{n^2} c_{i} f\big(\boldsymbol{\lambda}(A) +\boldsymbol{\lambda}(B)\big)= f\big(\boldsymbol{\lambda}(A) + \boldsymbol{\lambda}(B)\big). \end{align*} $$
Thus, the triangle inequality for f and (3.3) yield
4 Proof of Theorem 1.2
Let
![]() $\mathbf {X}$
be an iid random vector and define
$\mathbf {X}$
be an iid random vector and define
![]() $f_{\mathbf {X},d}:\mathbb {R}^n\to \mathbb {R}$
by
$f_{\mathbf {X},d}:\mathbb {R}^n\to \mathbb {R}$
by
 $$ \begin{align} f_{\mathbf{X},d}(\boldsymbol{\lambda}) = \left( \frac{\mathbb{E} |\langle\mathbf{X}, \boldsymbol{\lambda}\rangle|^d}{\Gamma(d+1)}\right)^{1/d} \quad \text{for }d \geq 1.\end{align} $$
$$ \begin{align} f_{\mathbf{X},d}(\boldsymbol{\lambda}) = \left( \frac{\mathbb{E} |\langle\mathbf{X}, \boldsymbol{\lambda}\rangle|^d}{\Gamma(d+1)}\right)^{1/d} \quad \text{for }d \geq 1.\end{align} $$
Since the entries of
![]() $\mathbf {X}$
are iid,
$\mathbf {X}$
are iid,
![]() $f_{\mathbf {X},d}$
is symmetric. In light of Theorem 1.1, it suffices to show that
$f_{\mathbf {X},d}$
is symmetric. In light of Theorem 1.1, it suffices to show that
![]() $f_{\mathbf {X},d}$
is a norm on
$f_{\mathbf {X},d}$
is a norm on
![]() $\mathbb {R}^n$
; the continuity remark at the end of Theorem 1.2 is Proposition 4.2.
$\mathbb {R}^n$
; the continuity remark at the end of Theorem 1.2 is Proposition 4.2.
Proposition 4.1 The function
![]() $f_{\mathbf {X},d}$
in (4.1) defines a norm on
$f_{\mathbf {X},d}$
in (4.1) defines a norm on
![]() $\mathbb {R}^n$
for all
$\mathbb {R}^n$
for all
![]() $d\geq 1$
.
$d\geq 1$
.
Proof The proofs for homogeneity and the triangle inequality in [Reference Chávez, Garcia and Hurley7, Section 3.1] are valid for
![]() $d\geq 1$
. However, the proof for positive definiteness in [Reference Chávez, Garcia and Hurley7, Lemma 3.1] requires
$d\geq 1$
. However, the proof for positive definiteness in [Reference Chávez, Garcia and Hurley7, Lemma 3.1] requires
![]() $d\geq 2$
. The proof below holds for
$d\geq 2$
. The proof below holds for
![]() $d\geq 1$
and is simpler than the original.
$d\geq 1$
and is simpler than the original.
Positive definiteness. If
![]() $f_{\mathbf {X},d}(\boldsymbol {\lambda })=0$
, then
$f_{\mathbf {X},d}(\boldsymbol {\lambda })=0$
, then
![]() $\mathbb {E}|\langle \mathbf {X},\boldsymbol {\lambda }\rangle |^d=0$
. The nonnegativity of
$\mathbb {E}|\langle \mathbf {X},\boldsymbol {\lambda }\rangle |^d=0$
. The nonnegativity of
![]() $|\langle \mathbf {X},\boldsymbol {\lambda }\rangle |^d$
ensures that
$|\langle \mathbf {X},\boldsymbol {\lambda }\rangle |^d$
ensures that
almost surely. Assume (4.2) has a nontrivial solution
![]() $\boldsymbol {\lambda }$
with nonzero entries
$\boldsymbol {\lambda }$
with nonzero entries
![]() $\lambda _{i_1}, \lambda _{i_2}, \ldots , \lambda _{i_k}$
. If
$\lambda _{i_1}, \lambda _{i_2}, \ldots , \lambda _{i_k}$
. If
![]() $k=1$
, then
$k=1$
, then
![]() $X_{i_k}=0$
almost surely, which contradicts the nondegeneracy of our random variables. If
$X_{i_k}=0$
almost surely, which contradicts the nondegeneracy of our random variables. If
![]() $k>1$
, then (4.2) implies that
$k>1$
, then (4.2) implies that
almost surely, in which
![]() $a_{i_j}=-\lambda _{i_j}/\lambda _{i_1}$
. The independence of
$a_{i_j}=-\lambda _{i_j}/\lambda _{i_1}$
. The independence of
![]() $X_{i_1}, X_{i_2}, \ldots , X_{i_k}$
contradicts (4.3). Relation (4.2) therefore has no nontrivial solutions.
$X_{i_1}, X_{i_2}, \ldots , X_{i_k}$
contradicts (4.3). Relation (4.2) therefore has no nontrivial solutions.
Homogeneity. This follows from the bilinearity of the inner product and linearity of expectation:
 $$ \begin{align*} f_{\mathbf{X},d}(c\boldsymbol{\lambda}) =\left( \frac{\mathbb{E} |c\langle\mathbf{X}, \boldsymbol{\lambda}\rangle|^d}{\Gamma(d+1)}\right)^{1/d} =\left(\frac{|c|^d\mathbb{E} |\langle\mathbf{X}, \boldsymbol{\lambda}\rangle|^d}{\Gamma(d+1)}\right)^{1/d} =|c|f_{\mathbf{X},d}(\boldsymbol{\lambda}). \end{align*} $$
$$ \begin{align*} f_{\mathbf{X},d}(c\boldsymbol{\lambda}) =\left( \frac{\mathbb{E} |c\langle\mathbf{X}, \boldsymbol{\lambda}\rangle|^d}{\Gamma(d+1)}\right)^{1/d} =\left(\frac{|c|^d\mathbb{E} |\langle\mathbf{X}, \boldsymbol{\lambda}\rangle|^d}{\Gamma(d+1)}\right)^{1/d} =|c|f_{\mathbf{X},d}(\boldsymbol{\lambda}). \end{align*} $$
Triangle inequality. For
![]() $\boldsymbol {\lambda }, \boldsymbol {\mu }\in \mathbb {R}^n$
, define random variables
$\boldsymbol {\lambda }, \boldsymbol {\mu }\in \mathbb {R}^n$
, define random variables
![]() $X=\langle \mathbf {X},\boldsymbol {\lambda }\rangle $
and
$X=\langle \mathbf {X},\boldsymbol {\lambda }\rangle $
and
![]() $Y=\langle \mathbf {X},\boldsymbol {\mu }\rangle $
. Minkowski’s inequality implies
$Y=\langle \mathbf {X},\boldsymbol {\mu }\rangle $
. Minkowski’s inequality implies
The triangle inequality for
![]() $f_{\mathbf {X},d}$
follows.
$f_{\mathbf {X},d}$
follows.
Proposition 4.2 Suppose
![]() $\mathbf {X}$
is an iid random vector whose entries have at least m moments. The function
$\mathbf {X}$
is an iid random vector whose entries have at least m moments. The function
![]() $f:\left [1,m\right ] \to \mathbb {R}$
defined by
$f:\left [1,m\right ] \to \mathbb {R}$
defined by
![]() $f(d) =\| A \|_{\mathbf {X},d}$
is continuous for all
$f(d) =\| A \|_{\mathbf {X},d}$
is continuous for all
![]() $A\in \mathrm {H}_n$
.
$A\in \mathrm {H}_n$
.
Proof Define the random variable
![]() $Y = \langle \mathbf {X}, \boldsymbol {\lambda }\rangle $
, in which
$Y = \langle \mathbf {X}, \boldsymbol {\lambda }\rangle $
, in which
![]() $\boldsymbol {\lambda }$
denotes the vector of eigenvalues of A. The random variable Y is a measurable function defined on a probability space
$\boldsymbol {\lambda }$
denotes the vector of eigenvalues of A. The random variable Y is a measurable function defined on a probability space
![]() $(\Omega , \mathcal {F}, \mathbb {P})$
. The pushforward measure of Y is the probability measure
$(\Omega , \mathcal {F}, \mathbb {P})$
. The pushforward measure of Y is the probability measure
![]() $\mu _{Y}$
on
$\mu _{Y}$
on
![]() $\mathbb {R}$
defined by
$\mathbb {R}$
defined by
![]() $\mu _Y(E)=\mathbb {P} (Y^{-1}(E) )$
for all Borel sets E. Consequently,
$\mu _Y(E)=\mathbb {P} (Y^{-1}(E) )$
for all Borel sets E. Consequently,
The bound
![]() $|x|^d \leq |x| + |x|^m$
holds for all
$|x|^d \leq |x| + |x|^m$
holds for all
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $1 \leq d \leq m$
. Therefore,
$1 \leq d \leq m$
. Therefore,
If
![]() $d_i\to d$
, then
$d_i\to d$
, then
![]() $\int |x|^{d_i}d\mu _Y\to \int |x|^{d}d\mu _Y$
by the dominated convergence theorem. Consequently,
$\int |x|^{d_i}d\mu _Y\to \int |x|^{d}d\mu _Y$
by the dominated convergence theorem. Consequently,
![]() $ \Gamma (d_i+1) (f(d_i) )^{d_i}\to \Gamma (d+1) (f(d) )^d $
whenever
$ \Gamma (d_i+1) (f(d_i) )^{d_i}\to \Gamma (d+1) (f(d) )^d $
whenever
![]() $d_i\to d$
. The function
$d_i\to d$
. The function
![]() $\Gamma (d+1) (f(d) )^d$
is therefore continuous in d. The continuity of the gamma function establishes continuity for
$\Gamma (d+1) (f(d) )^d$
is therefore continuous in d. The continuity of the gamma function establishes continuity for
![]() $f^d$
and f.
$f^d$
and f.
5 Remarks
Remark 5.1 A norm
![]() $\| \cdot \|$
on
$\| \cdot \|$
on
![]() $\mathrm {M}_n$
is weakly unitarily invariant if
$\mathrm {M}_n$
is weakly unitarily invariant if
![]() $\| A \|=\| U^*AU \|$
for all
$\| A \|=\| U^*AU \|$
for all
![]() $A\in \mathrm {M}_n$
and unitary
$A\in \mathrm {M}_n$
and unitary
![]() $U \in \mathrm {M}_n$
. A norm
$U \in \mathrm {M}_n$
. A norm
![]() $\Phi $
on the space
$\Phi $
on the space
![]() $C(S)$
of continuous functions on the unit sphere
$C(S)$
of continuous functions on the unit sphere
![]() $S\subset \mathbb {C}^n$
is a unitarily invariant function norm if
$S\subset \mathbb {C}^n$
is a unitarily invariant function norm if
![]() $\Phi (f\circ U)=\Phi (f)$
for all
$\Phi (f\circ U)=\Phi (f)$
for all
![]() $f\in C(S)$
and unitary
$f\in C(S)$
and unitary
![]() $U \in \mathrm {M}_n$
. Every weakly unitarily invariant norm
$U \in \mathrm {M}_n$
. Every weakly unitarily invariant norm
![]() $\| \cdot \|$
on
$\| \cdot \|$
on
![]() $\mathrm {M}_n$
is of the form
$\mathrm {M}_n$
is of the form
![]() $\| A \|=\Phi (f_A)$
, in which
$\| A \|=\Phi (f_A)$
, in which
![]() $f_A\in C(S)$
is defined by
$f_A\in C(S)$
is defined by
![]() $f_A(\mathbf {x})=\langle A\mathbf {x},\mathbf {x}\rangle $
and
$f_A(\mathbf {x})=\langle A\mathbf {x},\mathbf {x}\rangle $
and
![]() $\Phi $
is a unitarily invariant function norm [Reference Bhatia and Holbrook4], [Reference Bhatia3, Theorem 2.1].
$\Phi $
is a unitarily invariant function norm [Reference Bhatia and Holbrook4], [Reference Bhatia3, Theorem 2.1].
Remark 5.2 Remark 3.4 of [Reference Chávez, Garcia and Hurley7] is somewhat misleading. We state there that the entries of
![]() $\mathbf {X}$
are required to be identically distributed but not independent. To clarify, the entries of
$\mathbf {X}$
are required to be identically distributed but not independent. To clarify, the entries of
![]() $\mathbf {X}$
being identically distributed guarantee that
$\mathbf {X}$
being identically distributed guarantee that
![]() $\| \cdot \|_{\mathbf {X},d}$
satisfies the triangle inequality on
$\| \cdot \|_{\mathbf {X},d}$
satisfies the triangle inequality on
![]() $\mathrm {H}_n$
. The additional assumption of independence guarantees that
$\mathrm {H}_n$
. The additional assumption of independence guarantees that
![]() $\| \cdot \|_{\mathbf {X},d}$
is also positive definite.
$\| \cdot \|_{\mathbf {X},d}$
is also positive definite.
Acknowledgment
We thank the referee for many helpful comments.