A Note on a Fully Ordered Ring

Kwangil Koh

doi:10.4153/CMB-1967-083-8

A Note on a Fully Ordered Ring

Published online by Cambridge University Press: 20 November 2018

Kwangil Koh

Show author details

Kwangil Koh*: Affiliation:
North Carolina State University, Raleigh

Article contents

Extract
References

Rights & Permissions

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

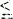A ring R (associative ring) is said to be fully ordered provided that R is a linearly ordered set under a relation such that for any a, b and c in R, 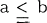implies that 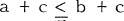and if c ε 0 then 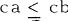and 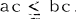. We say a subset K of R is convex provided that if a, b ε K such that 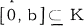then the interval [a, b] is a subset of K. Obviously an additive subgroup K of R is convex if and only if b ε K and b > 0 implies [a, b] ⊆ K.