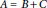Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kȩpczyk, Marek
2017.
A ring which is a sum of two PI subrings is always a PI ring.
Israel Journal of Mathematics,
Vol. 221,
Issue. 1,
p.
481.
Kȩpczyk, Marek
2020.
Rings which are sums of PI subrings.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 08,
p.
2050157.
Kȩpczyk, Marek
and
Mazurek, Ryszard
2020.
On the Representation of Fields as Finite Sums of Proper Subfields.
Results in Mathematics,
Vol. 75,
Issue. 2,
Kȩpczyk, Marek
2021.
Note on rings which are sums of a subring and an additive subgroup.
Applicable Algebra in Engineering, Communication and Computing,
Vol. 32,
Issue. 3,
p.
359.
Kȩpczyk, Marek
2022.
On rings which are sums of subrings and additive subgroups.
International Journal of Algebra and Computation,
Vol. 32,
Issue. 06,
p.
1203.
Kȩpczyk, Marek
2024.
On the representation of fields as sums of two proper subfields.
International Journal of Algebra and Computation,
Vol. 34,
Issue. 07,
p.
993.