Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bryant, Jack
and
Guseman, L. F.
1973.
Extensions of Contractive Mappings and Edelstein's Iterative Test.
Canadian Mathematical Bulletin,
Vol. 16,
Issue. 2,
p.
185.
Solomon, J. L.
1973.
A note on the extension of contractive mappings.
Proceedings of the American Mathematical Society,
Vol. 40,
Issue. 1,
p.
319.
Janos, Ludvik
1975.
On the Edelstein Contractive Mapping Theorem.
Canadian Mathematical Bulletin,
Vol. 18,
Issue. 5,
p.
675.
Ivanov, A. A.
1979.
Fixed points of mappings of metric spaces.
Journal of Soviet Mathematics,
Vol. 12,
Issue. 1,
p.
1.
Ding, Changming
and
Nadler, S.B.
2002.
The periodic points and the invariant set of an ϵ-contractive map.
Applied Mathematics Letters,
Vol. 15,
Issue. 7,
p.
793.
Baronti, Marco
Casini, Emanuele
and
Papini, Pier Luigi
2006.
Diametrically contractive maps and fixed points.
Fixed Point Theory and Applications,
Vol. 2006,
Issue. 1,
Pazdera, Jaroslav
Schumacher, J. M.
and
Werker, Bas J. M.
2013.
Intra-Group Risk Sharing Under Financial Fairness.
SSRN Electronic Journal,
Bao, Hailong
Ponds, Eduard H.M.
and
Schumacher, J. M.
2015.
Multi-Period Risk Sharing Under Financial Fairness.
SSRN Electronic Journal,
Bao, Hailong
Ponds, Eduard H.M.
and
Schumacher, Johannes M.
2017.
Multi-period risk sharing under financial fairness.
Insurance: Mathematics and Economics,
Vol. 72,
Issue. ,
p.
49.
Pazdera, Jaroslav
Schumacher, Johannes M.
and
Werker, Bas J.M.
2017.
The composite iteration algorithm for finding efficient and financially fair risk-sharing rules.
Journal of Mathematical Economics,
Vol. 72,
Issue. ,
p.
122.
Schumacher, Johannes M.
2018.
A Multi-Objective Interpretation of Optimal Transport.
Journal of Optimization Theory and Applications,
Vol. 176,
Issue. 1,
p.
94.
Niakh, Fallou
2025.
A fixed point approach for computing actuarially fair Pareto optimal risk-sharing rules.
European Actuarial Journal,
Vol. 15,
Issue. 1,
p.
297.
Ng, Tak Wa
and
Nguyen, Thai
2025.
Pareto efficiency and financial fairness under limited expected loss constraint.
Journal of Mathematical Economics,
Vol. 117,
Issue. ,
p.
103096.
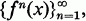 where f 1(x)=f(x) and f n(x)=f(f n-1(x)) for each n>1, is called the sequence of iterates of f at x.
where f 1(x)=f(x) and f n(x)=f(f n-1(x)) for each n>1, is called the sequence of iterates of f at x.
