Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bradley, David M.
2018.
Concerning an infinite series of Ramanujan related to the natural logarithm.
The Ramanujan Journal,
Vol. 47,
Issue. 2,
p.
253.
Irshad, Nazia
Khan, Asif R.
Mehmood, Faraz
and
Pečarić, Josip
2021.
New Perspectives on the Theory of Inequalities for Integral and Sum.
p.
193.

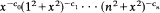 completely monotone?”
completely monotone?”