Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-15T06:46:40.476Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Endomorphism Semigroups

Published online by Cambridge University Press:  20 November 2018

Craig Platt
Craig Platt*
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 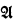is a universal algebra, the set of endomorphisms of 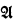forms a monoid (i.e., semigroup with identity) under composition. We denote it by End (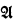). For definitions and notations, see [1]. It is well known (e.g., [1], Theorem 12.3) that for any monoid M there is a unary algebra 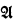with M ≅ End (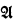). E. Mendelsohn and Z. Hedrlin [3] have proved that the monoid of a subalgebra of an algebra 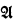is independent of the monoid of 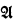. In [2], Hedrlin proves the same for the monoid of a homomorphic image of 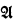. The proofs of these depend heavily on graph-theoretical and category-theoretical considerations. In this note considerably shorter direct algebraic proofs are given of these results.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 1 , March 1970 , pp. 47 - 48
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Grätzer, G., Universal Algebra, Van Nostrand, 1968.Google Scholar
2. Hedrlín, Z., On endomorphisms of graphs and their homomorphic images, to appear in Proof Techniques in Graph Theory, forthcoming, Academic Press.Google Scholar
3. Hedrlín, Z., and Mendelsohn, E., On the category of graphs with a given subgraph, to appear in the Canadian Journal of Mathematics.Google Scholar
4. Hedrlín, Z., and Pultr, A., On full embeddings of categories of algebras, Illinois Journal of Mathematics 10 (1966), 392-406.Google Scholar