Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T06:02:38.720Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Fine Graphs and Homological Isoperimetric Inequalities

Published online by Cambridge University Press:  20 November 2018

Eduardo Martínez-Pedroza
Eduardo Martínez-Pedroza*
Affiliation:
Memorial University, St. John’s, Newfoundland A1C 5S7 e-mail: emartinezped@mun.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the framework of homological characterizations of relative hyperbolicity, Groves and Manning posed the question of whether a simply connected 2-complex 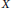$X$ with a linear homological isoperimetric inequality, a bound on the length of attachingmaps of 2-cells, and finitely many 2-cells adjacent to any edge must have a fine 1-skeleton. We provide a positive answer to this question. We revisit a homological characterization of relative hyperbolicity and show that a group 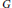$G$ is hyperbolic relative to a collection of subgroups 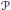$P$ if and only if 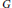$G$ acts cocompactly with finite edge stabilizers on a connected 2-dimensional cell complex with a linear homological isoperimetric inequality and 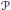$P$ is a collection of representatives of conjugacy classes of vertex stabilizers.

Keywords

20F6705C1020J0557M60isoperimetric functionsDehn functionshyperbolic groups
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 170 - 181
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Bowditch, B. H., Relatively hyperbolic groups. Internat. J. Algebra Comput. 22(2012), no. 3, 1250016. http://dx.doi.Org/10.1142/S0218196712500166 Google Scholar
[2] Bridson, M. R. and Haefliger, A.. Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften, 319, Springer-Verlag, Berlin, 1999.Google Scholar
[3] Dahmani, F., Les groupes relativement hyperboliques et leurs bords. PhD thesis, Université Louis Pasteur, Strasbourg, France, 2003.Google Scholar
[4] Gersten, S. M., A cohomological characterisation of hyperbolic groups. http://www.math.utah.eduA-sg/Papers/ch.pdf Google Scholar
[5] Gersten, S. M., Homological dehn functions and the word problem. http://www.math.utah.edu/∼sg/Papers/df9.pdf Google Scholar
[6] Gersten, S. M., Subgroups of word hyperbolic groups in dimension 2. J. London Math. Soc. (2) 54(1996), no. 2, 261–283. http://dx.doi.Org/10.1112/jlms/54.2.261 Google Scholar
[7] Gersten, S. M., Cohomological lower bounds for isoperimetric functions on groups. Topology 37(1998), no. 5, 1031–1072. http://dx.doi.Org/10.1016/S0040-9383(97)00070-0 Google Scholar
[8] Gromov, M.. Hyperbolic groups. In: Essays in group theory, Math. Sci. Res. Inst. Publ., 8, Springer, New York, 1987, pp. 75–263.Google Scholar
[9] Groves, D. and Manning, J. F., Dehn filling in relatively hyperbolic groups. Israel J. Math. 168(2008), 317–429. http://dx.doi.Org/10.1007/s11856-008-1070-6 Google Scholar
[10] Hruska, G. C., Relative hyperbolicity and relative quasiconvexity for countable groups. Algebr. Geom. Topol. 10(2010), no. 3, 1807–1856. http://dx.doi.Org/10.2140/agt.2010.10.1807 Google Scholar
[11] Martinez-Pedroza, E.. Subgroups of relatively hyperbolic groups ofbredon cohomological dimension 2. arxiv:1 508.04865Google Scholar
[12] Martinez-Pedroza, E. and Wise, D. T., Local quasiconvexity of groups acting on small cancellation complexes. J. Pure Appl. Algebra 215(2011), no. 10, 2396–2405. http://dx.doi.Org/10.1016/j.jpaa.2O10.12.019 Google Scholar
[13] Martinez-Pedroza, E. and Wise, D. T., Relative quasiconvexity using fine hyperbolic graphs. Algebr. Geom. Topol. 11(2011), 477–501. http://dx.doi.Org/10.21 4O/agt.2O11.11.477 Google Scholar
[14] Mineyev, I., Bounded cohomology characterizes hyperbolic groups. Q. J. Math. 53(2002), no. 1, 59–73. http://dx.doi.Org/10.1093/qjmath/53.1.59 Google Scholar
[15] Mineyev, I. and Yaman, A.. Relative hyperbolicity and bounded cohomology. http://www.math.uiuc.edu/-mineyev/math/art/rel-hyp.pdf Google Scholar
[16] Osin, D. V., Relatively hyperbolic groups: intrinsic geometry, algebraic properties, and algorithmic problems. Mem. Amer. Math. Soc. 179(2006), no. 843.Google Scholar