Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Daigle, Daniel
2020.
Locally nilpotent derivations and the structure of rings.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 4,
p.
106201.

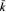 is solvable over
is solvable over 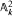 is geometrically factorial and hence isomorphic to
is geometrically factorial and hence isomorphic to 