Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T02:44:12.930Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the Number of Solutions of f(x1) = f(x2) = … =f(xr) over a Finite Field

Published online by Cambridge University Press:  20 November 2018

Kenneth S. Williams
Kenneth S. Williams*
Affiliation:
Carleton University, Ottawa, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let GF(q) denote the finite field with q = pn elements and let

(1)

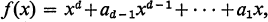
where each ai ∊ GF(q) and 1 < d <p. For r=2, 3, …, d we let nr denote the number of solutions (x1, …, xr) over GF(q) of

(2)

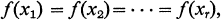
for which x1, …, xr are all different. Birch and Swinnerton-Dyer [1] have shown that

(3)

where each vr is a nonnegative integer depending on f and q and the constant implied by the O-symbol depends here, and throughout the paper, only on d.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 14 , Issue 3 , September 1971 , pp. 429 - 432
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Birch, B. J. and Swinnerton-Dyer, H. P. F., Note on a problem of Chowla, Acta Arith. 5 (1959), 417-423.Google Scholar
2. Chalk, J. H. H. and Williams, K. S., The distribution of solutions of congruences, Mathematika 12 (1965), 176-192.Google Scholar
3. Williams, K. S., On extremal polynomials, Canad. Math. Bull. 10 (1967), 585-594.Google Scholar