Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T11:25:27.506Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the phase retrieval of holomorphic functions

Part of: Spaces and algebras of analytic functions Entire and meromorphic functions, and related topics Communication, information

Published online by Cambridge University Press:  08 October 2020

Rolando Perez III
Rolando Perez III*
Affiliation:
Université de Bordeaux, CNRS, Bordeaux INP, IMB, UMR 5251, F-33400Talence, France and Institute of Mathematics, University of the Philippines Diliman, 1101 Quezon City, Philippines
*
e-mail:roperez@u-bordeaux.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that if f and g are holomorphic functions on an open connected domain, with the same moduli on two intersecting segments, then 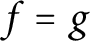$f=g$ up to the multiplication of a unimodular constant, provided the segments make an angle that is an irrational multiple of 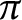$\pi $ . We also prove that if f and g are functions in the Nevanlinna class, and if 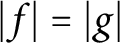$|f|=|g|$ on the unit circle and on a circle inside the unit disc, then 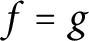$f=g$ up to the multiplication of a unimodular constant.

Keywords

Phase retrievalholomorphic functions

MSC classification

Primary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Secondary: 30H10: Hardy spaces 30H15: Nevanlinna class and Smirnov class 94A12: Signal theory (characterization, reconstruction, filtering, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 779 - 786
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported by the CHED-PhilFrance scholarship from Campus France and the Commission of Higher Education (CHED), Philippines.

References

Akutowicz, E. J., On the determination of the phase of a Fourier integral. I . Trans. Amer. Math. Soc. 83(1956), 179–192. http://dx.doi.org/10.2307/1992910 Google Scholar
Akutowicz, E. J., On the determination of the phase of a Fourier integral. II . Proc. Amer. Math. Soc. 8(1957), 234–238. http://dx.doi.org/10.2307/2033718 Google Scholar
Boche, H., Li, N., and Pohl, V., Phase retrieval in spaces of analytic functions on the unit disk . In: 2017 International Conference on Sampling Theory and Applications (SampTA), Tallin, 2017, pp. 336–340. http://dx.doi.org/10.1109/SAMPTA.2017.8024411 Google Scholar
Bodmann, B. and Hammen, N., Stable phase retrieval with low redundancy frames . Adv. Comput. Math. 41(2015), 317–331. http://dx.doi.org/10.1007/s10444-014-9359-y CrossRefGoogle Scholar
Duren, P., The theory of ${H}^p$ spaces. Academic Press, New York, 1970.Google Scholar
Grohs, P., Koppensteiner, S., and Rathmair, M., Phase retrieval: uniqueness and stability . SIAM Rev. 62(2020), 301–350. http://dx.doi.org/10.1137/19M1256865 CrossRefGoogle Scholar
Grohs, P. and Rathmair, M., Stable Gabor phase retrieval and spectral clustering . Comm. Pure Appl. Math. 72(2019), 981–1043. http://dx.doi.org/10.1002/cpa.21799 CrossRefGoogle Scholar
Hofstetter, E., Construction of time-limited functions with specified autocorrelation functions . IEEE Trans. Inform. Theory 10(1964), 119–126. http://dx.doi.org/10.1109/TIT.1964.1053648 CrossRefGoogle Scholar
Jaming, P., Uniqueness results in an extension of Pauli’s phase retrieval problem . Appl. Comput. Harmon. Anal. 37(2014), 413–441. http://dx.doi.org/10.1016/j.acha.2014.01.003 CrossRefGoogle Scholar
Jaming, P., Kellay, K., and Perez, R. III, Phase retrieval for wide band signals . J. Fourier Anal. Appl. 26(2020), Paper No. 54. http://dx.doi.org/10.1007/s00041-020-09767-1 CrossRefGoogle Scholar
Klibanov, M., Sacks, P., and Tikhonravov, A., The phase retrieval problem . Inverse Prob. 11(1995), 1–28.CrossRefGoogle Scholar
McDonald, J., Phase retrieval and magnitude retrieval of entire functions . J. Fourier Anal. Appl. 10(2004), 259–267. http://dx.doi.org/10.1007/s00041-004-0973-9 CrossRefGoogle Scholar
Nikolski, N., Hardy spaces . Cambridge Studies in Advanced Mathematics , 179, Cambridge University Press, Cambridge, UK, 2019.Google Scholar
Waldspurger, I. and Mallat, S., Phase retrieval for the Cauchy wavelet transform . J. Fourier Anal. Appl. 21(2015), 1251–1309. http://dx.doi.org/10.1007/s00041-015-9403-4 Google Scholar
Walther, A., The question of phase retrieval in optics . Optica Acta 10(1963), 41–49. http://dx.doi.org/10.1080/713817747 CrossRefGoogle Scholar