Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-11T00:29:26.928Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Universe of a Category of Fractions

Published online by Cambridge University Press:  20 November 2018

Sribatsa Nanda
Sribatsa Nanda*
Affiliation:
Mathematics Department, Regional Engineering College, Rourkela-8 (Orissa), India 769008
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

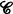Let be a small 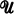-category where 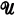is a fixed Grothendieck universe, i.e., the objects of 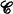form a set which is a subset of 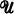and, for every pair of objects 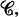X, Y of the set 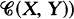is an element of 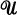. If S is a set of morphisms of , then, in general, the category of fractions 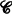[S- 1] would belong to a higher universe ([4], p. 256).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 4 , 01 December 1980 , pp. 425 - 427
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Deleanu, A., Existence of the Adams completion for CW-complexes, J. Pure and App. Alg. 4 (1974), 299-308.Google Scholar
2. A Deleanu, Existence of the Adams completion for objects of cocomplete categories, J. Pure and App. Alg. 6 (1975), 31-39.Google Scholar
3. Nanda, S., Adams cocompletion and the minimal model (preprint).Google Scholar
4. Schubert, H., Categories, Springer, Berlin (1972).Google Scholar
5. Switzer, R. M., Algebraic Topology-Homotopy and Homology, Springer, Berlin (1975).Google Scholar