Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T05:04:18.243Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Toric Varieties Associated with Moduli Spaces

Published online by Cambridge University Press:  20 November 2018

James J. Uren
James J. Uren*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 3G3 e-mail: jjuren@math.toronto.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we give a brief review of the construction of a toric variety 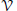$\mathcal{V}$ coming from a genus 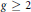$g\,\ge \,2$ Riemann surface 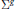${{\sum }^{g}}$ equipped with a trinion, or pair of pants, decomposition. This was outlined by J. Hurtubise and L. C. Jeffrey. A. Tyurin used this construction on a certain collection of trinion decomposed surfaces to produce a variety 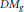$D{{M}_{g,}}$ the so-called Delzant model of moduli space, for each genus $g$. We conclude this note with some basic facts about the moment polytopes of the varieties 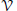$\mathcal{V}$. In particular, we show that the varieties 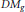$D{{M}_{g}}$ constructed by Tyurin, and claimed to be smooth, are in fact singular for 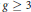$g\,\ge \,3$.

Keywords

14M2552B20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 3 , 01 September 2011 , pp. 561 - 565
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Goldman, W. M., The symplectic nature of fundamental groups of surfaces. Adv. in Math. 54(1984), no. 2, 200–225. doi:10.1016/0001-8708(84)90040-9Google Scholar
[2] Hurtubise, J. and Jeffrey, L. C., Representations with weighted frames and framed parabolic bundles. Canad. J. Math. 52(2000), no. 6, 1235–1268.Google Scholar
[3] Jeffrey, L. C. and Weitsman, J., Bohr-Sommerfeld orbits in the moduli space of flat connections and the Verlinde dimension formula. Commun. Math. Phys. 150(1992), no. 3, 593–630. doi:10.1007/BF02096964Google Scholar
[4] Jeffrey, L. C. and Weitsman, J., Toric structures on the moduli space of flat connections on a Riemann surface: volumes and the moment map. Adv. Math. 106(1994), no. 2, 151–168. doi:10.1006/aima.1994.1054Google Scholar
[5] Tyurin, A. N., Delzant models of moduli spaces. (Russian) Izv. Ross. Akad. Nauk. Ser. Mat. 67(2003), no. 2, 167–180.Google Scholar