Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Forsythe, David P.
1972.
The UN and the Arab-Israeli Conflict: What has been Learned in 25 Years?.
International Organization,
Vol. 26,
Issue. 4,
p.
705.
Croft, Hallard T.
Falconer, Kenneth J.
and
Guy, Richard K.
1991.
Unsolved Problems in Geometry.
Vol. 2,
Issue. ,
p.
48.
FLORIAN, A.
1993.
Handbook of Convex Geometry.
p.
177.


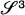 of all polyhedra with triangular faces then for all
of all polyhedra with triangular faces then for all