Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T06:54:03.872Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Certain Set of Linear Inequalities

Published online by Cambridge University Press:  20 November 2018

J.G. Kalbfleisch  and
R. G. Stanton
J.G. Kalbfleisch
Affiliation:
York University, Toronto
R. G. Stanton
Affiliation:
York University, Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall discuss the following set of n + 1 linear inequalities:

If we let 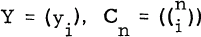, and Z = (zi) (i = 0, 1,…, n) be (n+1)-dimensional column vectors, and define the n+1 by n+1 tridiagonal matrix Dn(ϕ) by

the set of inequalities (1) may be written

where An= Dn(1) and zi≥ 0 (i = 0, 1,…, n). In sections 2 and 3, we

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 5 , December 1968 , pp. 681 - 690
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Cox, D.R. and Miller, H.D., The theory of stochastic processes. (Methuen and Co. Ltd., London, 1965) 129-132.Google Scholar
2. Henrici, P., Discrete variable methods in ordinary differential equations. (Wiley, 1962).Google Scholar
3. Kac, Mark, Random walk and the theory of Brownian motion, American Mathematical Monthly 54 (1947), 369-391.Google Scholar
4. Stanton, R.G. and Kalbfleisch, J. G., Covering problems for dichotomized matchings. Aequationes Mathematicae 1 (1968) 94-103.Google Scholar
5. Sylvester, J.J., Théorème sur les déterminants de M. Sylvester, Nouv. Annales de Math. 13 (1854) 305.Google Scholar