Published online by Cambridge University Press: 20 November 2018
Kaplansky's Lemma [3] states: the number of k-combinations of 1, 2,…, n with no two consecutive integers in any selection is 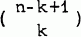 Using this, Abramson [l; lemma 3] solves the problem: find the, number of k-combinations so that no two integers i and i+2 appear in any selection. (This is generalized by Abramson in [2].) An interesting solution, also using Kaplansky's lemma, is obtained as follows.
Using this, Abramson [l; lemma 3] solves the problem: find the, number of k-combinations so that no two integers i and i+2 appear in any selection. (This is generalized by Abramson in [2].) An interesting solution, also using Kaplansky's lemma, is obtained as follows.
If n = 2m, we choose s from among the m even integer s, no two consecutive, and k- s from among the m odd integers, no two consecutive.