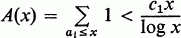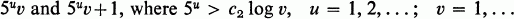Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ruzsa, I. Z.
1978.
On the additive completion of linear recurrence sequences.
Periodica Mathematica Hungarica,
Vol. 9,
Issue. 4,
p.
285.
Guy, Richard K.
1981.
Unsolved Problems in Number Theory.
p.
110.
Leth, Steven C.
1988.
Sequences in countable nonstandard models of the natural numbers.
Studia Logica,
Vol. 47,
Issue. 3,
p.
243.
Guy, Richard K.
1994.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
199.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
311.
Mauldin, R. Daniel
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
365.