Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T21:02:02.790Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Problem of Rubel Concerning the Set of Functions Satisfying All the Algebraic Differential Equations Satisfied by a Given Function

Published online by Cambridge University Press:  20 November 2018

John Shackell
John Shackell*
Affiliation:
Institute of Mathematics and Statistics The University Canterbury Kent CT2 7NF England, e-mail: J.R.Shackell@ukc.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For two functions 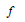$f$ and 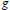$g$, define 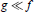$g\ll f$ to mean that 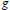$g$ satisfies every algebraic differential equation over the constants satisfied by 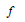$f$. The order 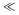$\ll $ was introduced in one of a set of problems on algebraic differential equations given by the late Lee Rubel. Here we characterise the set of 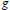$g$ such that 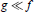$g\ll f$, when 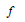$f$ is a given Liouvillian function.

Keywords

34A3412H05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 2 , 01 June 1998 , pp. 214 - 224
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Ritt, J. F., Differential Algebra. Amer. Math. Soc., 1950.Google Scholar
2. Rubel, L. A., Some research problems about algebraic differential equations. Trans. Amer. Math. Soc. 280 (1983), 43–52.Google Scholar
3. Shackell, J. R., Growth orders occurring in expansions of Hardy-field solutions of algebraic differential equations. Ann. Inst. Fourier 45 (1995), 183–221.Google Scholar
4. van der Waerden, B. J., Algebra, vol.2. Frederick Ungar Pub. Co., 1950.Google Scholar