Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T05:48:26.489Z Has data issue: false hasContentIssue false
  • English
  • Français

On an Exponential Functional Inequality and its Distributional Version

Published online by Cambridge University Press:  20 November 2018

Jaeyoung Chung
Jaeyoung Chung*
Affiliation:
Department of Mathematics, Kunsan National University, Kunsan, 573-701 Korea. e-mail: jychung@kunsan.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

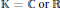Let $G$ be a group and $\mathbb{K}\,=\,\mathbb{C}\,\text{or}\,\mathbb{R}$. In this article, as a generalization of the result of Albert and Baker, we investigate the behavior of bounded and unbounded functions 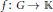$f\,:\,G\,\to \,\mathbb{K}$ satisfying the inequality

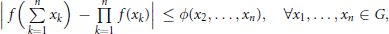$$\left| f\left( \sum\limits_{k=1}^{n}{{{x}_{k}}} \right)\,-\,\underset{k=1}{\overset{n}{\mathop{\Pi }}}\,f\left( {{x}_{k}} \right) \right|\,\,\le \phi \left( {{x}_{2}},\,.\,.\,.\,,{{x}_{n}} \right),\,\,\,\,\,\,\forall {{x}_{1}},\,.\,.\,.\,,{{x}_{n}}\,\in \,G,$$

Where 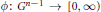$\phi :\,{{G}^{n-1}}\,\to \,[0,\,\infty )$. Also as a a distributional version of the above inequality we consider the stability of the functional equation

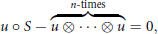$$u\,\circ \,S\,-\,\overbrace{u\,\otimes \,.\,.\,.\,\otimes \,u}^{n-\text{times}}\,=\,0,$$

where $u$ is a Schwartz distribution or Gelfand hyperfunction, $\circ$ and 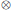$\otimes$ are the pullback and tensor product of distributions, respectively, and 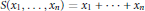$S\left( {{x}_{1}},\,.\,.\,.\,,{{x}_{n}} \right)\,=\,{{x}_{1}}\,+\,.\,.\,.\,+\,{{x}_{n}}$.

Keywords

46F9939B82distributionexponential functional equationGelfand hyperfunctionstability
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 30 - 43
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Acz´el, J. and Dhombres, J., Functional equations in several variables. Cambridge University Press, New York–Sydney, 1989.Google Scholar
[2] Albert, M. and Baker, J. A., Bounded solutions of a functional inequality. Canad. Math. Bull. 25 (1982), 491–495. http://dx.doi.org/10.4153/CMB-1982-071-9 Google Scholar
[3] Baker, J. A., The stability of cosine functional equation. Proc. Amer. Math. Soc. 80 (1980), 411–416. http://dx.doi.org/10.1090/S0002-9939-1980-0580995-3 Google Scholar
[4] Gelfand, I. M. and Shilov, G. E., Generalized functions II. Academic Press, New York, 1968.Google Scholar
[5] Gelfand, I. M. and Shilov, G. E., Generalized functions IV. Academic, Press, New York, 1968.Google Scholar
[6] Hörmander, L., The analysis of linear partial differential operators I. Springer-Verlag, Berlin–New York, 1983.Google Scholar
[7] Hyers, D. H., On the stability of the linear functional equations. Proc. Nat. Acad. Sci. USA 27 (1941), 222–224. http://dx.doi.org/10.1073/pnas.27.4.222 Google Scholar
[8] Hyers, D. H., Isac, G. and Rassias, Th. M., Stability of functional equations in several variables. Birkhauser, Boston, 1998.Google Scholar
[9] Jung, S. M., Hyers–Ulam-Rassias Stability of Functional Equations in Nonlinear Analysis. Springer, New York, 2011.Google Scholar
[10] Matsuzawa, T., A calculus approach to hyperfunctions II. Trans. Amer. Math. Soc. 313 (1989), 619–654. http://dx.doi.org/10.1090/S0002-9947-1989-0997676-7 Google Scholar
[11] Rassias, J. M., On Approximation of Approximately Linear Mappings by Linear Mappings. Bull. Sci. Math. 108 (1984), 445–446. Google Scholar
[12] Rassias, J. M., Solution of a problem of Ulam. J. Approx. Theory 57 (1989), 268–273. http://dx.doi.org/10.1016/0021-9045(89)90041-5 Google Scholar
[13] Rassias, Th. M., On the stability of functional equations in Banach spaces. J. Math. Anal. Appl. 251 (2000), 264–284. http://dx.doi.org/10.1006/jmaa.2000.7046 Google Scholar
[14] Rassias, Th. M., On the stability of the linear mapping in Banach spaces. Proc. Amer. Math. Soc. 7 (1978), 297–300. http://dx.doi.org/10.1090/S0002-9939-1978-0507327-1 Google Scholar
[15] Schwartz, L., Th´eorie des distributions. Hermann, Paris, 1966.Google Scholar
[16] Widder, D.V., The heat equation. Academic Press, New York, 1975.Google Scholar