Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T03:59:35.939Z Has data issue: false hasContentIssue false
  • English
  • Français

On Analytic Functions of Bergman BMO in the Ball

Published online by Cambridge University Press:  20 November 2018

E. G. Kwon
E. G. Kwon*
Affiliation:
Department of Mathematics Education Andong National University Andong 760-749 Korea
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

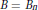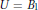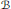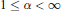Let $B\,=\,{{B}_{n}}$ be the open unit ball of ${{C}^{n}}$ with volume measure $v$, $U\,=\,{{B}_{1}}$ and $B$ be the Bloch space on $U.\,{{\mathcal{A}}^{2,\alpha }}(B)$, $1\,\le \,\alpha \,<\infty $, is defined as the set of holomorphic 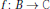$f\,:\,B\,\to \,C$ for which

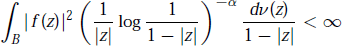$$\int_{B\,}{{{\left| f(z) \right|}^{2}}}{{\left( \frac{1}{\left| z \right|}\,\log \frac{1}{1\,-\left| z \right|} \right)}^{-\alpha }}\,\frac{dv(z)}{1\,-\,\left| z \right|}\,<\,\infty $$

if 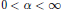$0\,<\,\alpha \,<\infty $ and 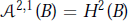${{\mathcal{A}}^{2,1}}(B)\,=\,{{H}^{2}}(B)$, the Hardy space. Our objective of this note is to characterize, in terms of the Bergman distance, those holomorphic $f\,:\,B\,\to \,U$ for which the composition operator 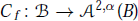${{C}_{f}}\,:\,B\,\to \,{{\mathcal{A}}^{2,\alpha }}(B)$ defined by 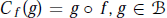${{C}_{f}}(g)=g\,\text{o}\,f\text{,}\,g\in B$, is bounded. Our result has a corollary that characterize the set of analytic functions of bounded mean oscillation with respect to the Bergman metric.

Keywords

32A37Bergman distanceBMOAHardy spaceBloch function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 1 , 01 March 1999 , pp. 97 - 103
Copyright
Copyright © Canadian Mathematical Society 1999

References

[CRW] Coifman, R., Rochberg, R. and Weiss, G., Factorization theorems for Hardy spaces in several variables. Ann. of Math. 103 (1976), 611–635.Google Scholar
[G] Garnett, J. B., Bounded analytic functions. Academic Press, New York, 1981.Google Scholar
[K1] Kwon, E. G., Composition of Blochs with bounded analytic functions. Proc. Amer. Math. Soc. 124 (1996), 1473–1480.Google Scholar
[K2] Kwon, E. G., Mean growth of the hyperbolic Hardy class functions. Math. Japon. 35 (1990), 451–460.Google Scholar
[P] Pavlović, M., Inequalities for the gradient of eigenfunctions of the invariant Laplacian. Indag. Math. (1) 2 (1991), 89–98.Google Scholar
[R] Rudin, W., Function Theory in the unit ball of Cn . Springer-Verlag, New York, 1980.Google Scholar
[RU] Ramey, Wade and Ullrich, David, Bounded mean oscillations of Bloch pullbacks. Math. Ann. 291 (1991), 591–606.Google Scholar
[Y1] Yamashita, Shinji, Hyperbolic Hardy class H1 . Math. Scand. 45 (1979), 261–266.Google Scholar
[Y2] Yamashita, Shinji, Holomorphic functions of hyperbolically bounded mean oscillation. Boll. Un. Mat. Ital. B (6) 5 (1986), 983–1000.Google Scholar