No CrossRef data available.
Article contents
On Carleman Integral Operators
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
L 2(a, b)
1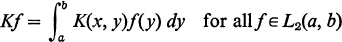
with the property
2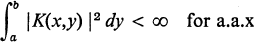
were originally defined by T. Carleman [4]. Here he imposed on the kernel the conditions of measurability and hermiticity,
3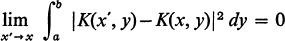
for all x with the exception of a countable set with a finite number of limit points and
4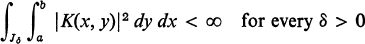
where J δ denotes the interval [a, b] with the exception of subintervals |x - ξv| < δ; here ξv represents a finite set of points for which (3) fails to hold.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1970
References
2.
Stone, M. H., Linear transformations in Hilbert space and their applications to analysis, American Math. Soc. Colloq. Publ., Vol. XV, New York, 1932.Google Scholar
3.
Korotkov, V. B., Integral operators with Carleman kernels, Differencial'nye Uravnenija
2, (1965), 252-265. (Math. Reviews Vol. 32 (1966), Part 2).Google Scholar
4.
Carleman, T., Sur les équations intégrales singulières à noyau reél et symétrique, Uppsala
1923.Google Scholar
5.
Carleman, T., La théorie des équations intégrales singulières et ses applications, Ann. Inst. H. Poincaré, 1931.Google Scholar
7.
Targonski, G. I., Seminar on functional operators and equations. Lecture Notes in Mathematics No. 33, Springer-Verlag, Berlin, 1962.Google Scholar

