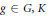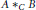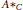Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Peterson, Jesse
and
Thom, Andreas
2011.
Group cocycles and the ring of affiliated operators.
Inventiones mathematicae,
Vol. 185,
Issue. 3,
p.
561.