No CrossRef data available.
Article contents
On Characterizations of Conditional Expectation
Published online by Cambridge University Press: 20 November 2018
Extract
In the following (Ω, α, μ) is a totally σ-finite measure space except where noted. For a sub-σ-algebra β ⊂ α, the conditional expectation E{f|β} off given β is a function measurable relative to β, such that
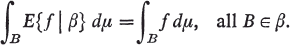
In [5] R.G.Douglas proved, among other things the following, in the finite case:
Suppose μ(Ω)=l. Then a linear operator T on L1(Ω, α,μ) is a conditional expect ion if and only if
1.1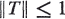
1.2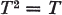
1.3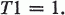
The point of this note is to characterize conditional expectation in the σ-finite case (Theorems 2, 3).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1973


