Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bruckner, Andrew M.
1976.
Derivatives: Why They Elude Classification.
Mathematics Magazine,
Vol. 49,
Issue. 1,
p.
5.
Peters, James F.
2011.
Multi-disciplinary Trends in Artificial Intelligence.
Vol. 7080,
Issue. ,
p.
1.
Ramanna, Sheela
and
Peters, James F.
2012.
Rough Sets: Selected Methods and Applications in Management and Engineering.
p.
181.
Peters, James F.
and
Ramanna, Sheela
2012.
Advances on Computational Intelligence.
Vol. 297,
Issue. ,
p.
586.


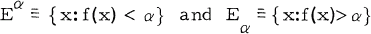 a remembers of P. Many classes of functions have been characterized in terms of associated sets. The chart below summarizes a few such characterizations.
a remembers of P. Many classes of functions have been characterized in terms of associated sets. The chart below summarizes a few such characterizations.