On Deformations of the Complex Structure on the Moduli Space of Spatial Polygons

Abstract

For an integer 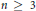$n\,\ge \,3$, let 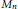${{M}_{n}}$ be the moduli space of spatial polygons with $n$ edges. We consider the case of odd $n$. Then 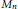${{M}_{n}}$ is a Fano manifold of complex dimension 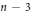$n\,-\,3$. Let 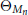${{\Theta }_{{{M}_{n}}}}$ be the sheaf of germs of holomorphic sections of the tangent bundle 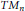$T{{M}_{n}}$. In this paper, we prove 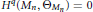${{H}^{q}}\left( {{M}_{n}},\,{{\Theta }_{{{M}_{n}}}} \right)\,=\,0$ for all 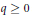$q\,\ge \,0$ and all odd $n$. In particular, we see that the moduli space of deformations of the complex structure on 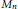${{M}_{n}}$ consists of a point. Thus the complex structure on 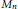${{M}_{n}}$ is locally rigid.