Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T10:39:34.102Z Has data issue: false hasContentIssue false
  • English
  • Français

On Gâteaux Differentiability of Pointwise Lipschitz Mappings

Published online by Cambridge University Press:  20 November 2018

Jakub Duda
Jakub Duda*
Affiliation:
Department of Mathematics, Weizmann Institute of Science, Rehovot 76100, Israel, e-mail: duda@karlin.mff.cuni.cz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that for every function 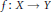$f\,:\,X\,\to \,Y$ , where 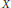$X$ is a separable Banach space and $Y$ is a Banach space with RNP, there exists a set 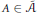$A\,\in \,\overset{\sim }{\mathop{\mathcal{A}}}\,$ such that 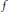$f$ is Gâteaux differentiable at all 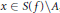$x\,\in \,S\left( f \right)\backslash A$, where 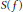$S\left( f \right)$ is the set of points where 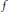$f$ is pointwise-Lipschitz. This improves a result of Bongiorno. As a corollary, we obtain that every 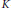$K$-monotone function on a separable Banach space is Hadamard differentiable outside of a set belonging to 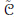$\tilde{C}\,;$ this improves a result due to Borwein and Wang. Another corollary is that if 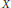$X$ is Asplund, 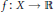$f\,:\,X\,\to \,\mathbb{R}$ cone monotone, 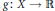$g\,:\,X\,\to \,\mathbb{R}$ continuous convex, then there exists a point in 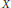$X$, where 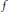$f$ is Hadamard differentiable and $g$ is Fréchet differentiable.

Keywords

46G0546T20Gâteaux differentiable functionRadon-Nikodým propertydifferentiability of Lipschitz functionspointwise-Lipschitz functionscone mononotone functions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 2 , 01 June 2008 , pp. 205 - 216
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Benyamini, Y. and Lindenstrauss, J., Geometric Nonlinear Functional Analysis. American Mathematical Society Colloquium Publications 48, American Mathematical Society, Providence, RI, 2000.Google Scholar
[2] Bongiorno, D., Stepanoff 's theorem in separable Banach spaces. Comment. Math. Univ. Carolin. 39(1998), no. 2, 323–335.Google Scholar
[3] Borwein, J. M., Burke, J. V., and Lewis, A. S., Differentiability of cone-monotone functions on separable Banach space. Proc. Amer. Math. Soc. 132(2004), no. 4, 1067–1076.Google Scholar
[4] Borwein, J. M. and Wang, X., Cone monotone functions: differentiability and continuity. Canadian J. Math. 57(2005), no. 5, 961–982.Google Scholar
[5] Deville, R., Godefroy, G., and Zizler, V., Smoothness and renormings in Banach spaces. Pitman Monographs and Surveys in Pure and Applied Mathematics 64, John Wiley, New York, 1993.Google Scholar
[6] Duda, J., Cone monotone mappings: continuity and differentiability. To appear in Nonlinear Anal.Google Scholar
[7] Lindenstrauss, J. and Preiss, D., On Fréchet differentiability of Lipschitz maps between Banach spaces. Ann. of Math. 157(2003), no. 1, 257–288.Google Scholar
[8] Preiss, D. and Zajíček, L., Directional derivatives of Lipschitz functions. Israel J. Math. 125(2001), 1–27.Google Scholar
[9] Rademacher, H., Über partielle und totale Differenziebarkeit. Math. Ann. 79(1919), 254–269.Google Scholar
[10] Stepanoff, W., Über totale Differenziebarkeit. Math. Ann. 90(1923), no. 3–4, 318–320.Google Scholar
[11] Stepanoff, W., Sur les conditions de l’existence de la differenzielle totale. Rec. Math. Soc. Math. Moscou 32 (1925), 511–526.Google Scholar
[12] Zajíček, L., On sets of non-differentiability of Lipschitz and convex functions. Math. Bohem. 132(2007), no. 1, 75..85.Google Scholar
[13] Zajíček, L., On σ-porous sets in abstract spaces. Abstr. Appl. Anal. 2005, no. 5, 509–534.Google Scholar