Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cheeger, Jeff
and
Gromov, Mikhael
1985.
Differential Geometry and Complex Analysis.
p.
115.
Sunada, Toshikazu
1988.
Geometry and Analysis on Manifolds.
Vol. 1339,
Issue. ,
p.
248.
Brüning, Jochen
and
Sunada, Toshikazu
1992.
On the spectrum of periodic elliptic operators.
Nagoya Mathematical Journal,
Vol. 126,
Issue. ,
p.
159.
Mathai, Varghese
1998.
Von Neumann Algebra Invariants of Dirac Operators.
Journal of Functional Analysis,
Vol. 152,
Issue. 1,
p.
1.
Post, Olaf
2001.
Partial Differential Equations and Spectral Theory.
p.
251.
Post, Olaf
2003.
Periodic manifolds with spectral gaps.
Journal of Differential Equations,
Vol. 187,
Issue. 1,
p.
23.
Post, Olaf
2003.
Eigenvalues in spectral gaps of a perturbed periodic manifold.
Mathematische Nachrichten,
Vol. 261-262,
Issue. 1,
p.
141.
Lenz, Daniel
and
Veselić, Ivan
2009.
Hamiltonians on discrete structures: jumps of the integrated density of states and uniform convergence.
Mathematische Zeitschrift,
Vol. 263,
Issue. 4,
p.
813.
Autunović, Tonći
and
Veselić, Ivan
2009.
Methods of Spectral Analysis in Mathematical Physics.
Vol. 186,
Issue. ,
p.
1.


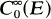 with respect to the inner product
with respect to the inner product 